题目内容
【题目】已知椭圆![]() 的上、下焦点分别为
的上、下焦点分别为![]() ,上焦点
,上焦点![]() 到直线
到直线![]() 的距离为3,椭圆
的距离为3,椭圆![]() 的离心率
的离心率![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)椭圆![]() ,设过点
,设过点![]() 斜率存在且不为0的直线交椭圆
斜率存在且不为0的直线交椭圆![]() 于
于![]() 两点,试问
两点,试问![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得 ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】分析:(1)根据已知列方程组,解方程组即得椭圆的方程. (2)先假设存在![]() ,再化简已知得到
,再化简已知得到![]() ,所以存在.
,所以存在.
详解:(1)由已知椭圆![]() 方程为
方程为![]() ,设椭圆的焦点
,设椭圆的焦点![]() ,
,
由![]() 到直线
到直线![]() 的距离为3,得
的距离为3,得![]() ,
,
又椭圆![]() 的离心率
的离心率![]() ,所以
,所以![]() ,又
,又![]() ,
,
求得![]() ,
,![]() .
.
椭圆![]() 方程为
方程为![]() .
.
(2)存在.理由如下:由(1)得椭圆![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,联立
,联立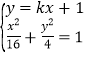 ,消去
,消去![]() 并整理得
并整理得![]() .
.
![]()
![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
假设存在点![]() 满足条件,由于
满足条件,由于![]() ,所以
,所以![]() 平分
平分![]() .
.
易知直线![]() 与直线
与直线![]() 的倾斜角互补,∴
的倾斜角互补,∴![]() .
.
即![]() ,即
,即![]() .(*)
.(*)
将![]() ,
,![]() 代入(*)并整理得
代入(*)并整理得![]() ,
,
∴![]() ,整理得
,整理得![]() ,即
,即![]() ,
,
∴当![]() 时,无论
时,无论![]() 取何值均成立. ∴存在点
取何值均成立. ∴存在点![]() 使得
使得![]() .
.

练习册系列答案
相关题目
【题目】某名校从2008年到2017年考入清华、北大的人数可以通过以下表格反映出来.(为了方便计算,将2008年编号为1,2009年编号为2,以此类推……)
年份 |
|
|
|
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
|
|
(1)根据最近5年的数据,利用最小二乘法求出![]() 与
与![]() 之间的线性回归方程,并用以预测2018年该校考入清华、北大的人数;(结果要求四舍五入至个位)
之间的线性回归方程,并用以预测2018年该校考入清华、北大的人数;(结果要求四舍五入至个位)
(2)从这10年的数据中随机抽取2年,记其中考入清华、北大的人数不少于![]() 的有
的有![]() 年,
年,
求![]() 的分布数列和数学期望.
的分布数列和数学期望.
参考公式: .
.
