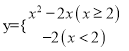Question

【题目】已知点(0,1),(3+2,0),(3-2,0)在圆C上.

(1)求圆C的方程.

(2)若圆C与直线x-y+a=0交于A,B两点,且OA⊥OB,求a的值.

Answer 1

【答案】（1）；（2）

【解析】试题分析：（1）设出圆的标准方程，把三个点代入，联立方程组求得．
（2）设出点的坐标，联立直线与圆的方程，消去，确定关于的一元二次方程，已知的垂直关系，确定，利用韦达定理求得a．

试题解析：(1) 设，由题意可设圆C的圆心为(3,t),则有32+(t-1)2=(2)2+t2,解得t=1.

则圆C的圆心为(3,1),半径长为=3，所以圆C的方程为(x-3)2+(y-1)2=9.

(2)由消去y,

得2x2+(2a-8)x+a2-2a+1=0,

此时判别式Δ=56-16a-4a2.设A(x1,y1),B(x2,y2),

则有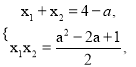　　　　　　①

由于OA⊥OB,可得x1x2+y1y2=0,又y1=x1+a,y2=x2+a,所以2x1x2+a(x1+x2)+a2=0,②

由①②得a=-1,满足Δ>0,故a=-1.