Question

【题目】设S，T是R的两个非空子集，如果存在一个从S到T的函数y=f（x）满足：（i）T={f（x）|x∈S}；（ii）对任意x1 ， x2∈S，当x1＜x2时，恒有f（x1）＜f（x2），那么称这两个集合“保序同构”，以下集合对不是“保序同构”的是（ ）
A.A=N* ， B=N
B.A={x|﹣1≤x≤3}，B={x|x=﹣8或0＜x≤10}
C.A={x|0＜x＜1}，B=R
D.A=Z，B=Q

Answer 1

【答案】D
【解析】解：对于A=N* ， B=N，存在函数f（x）=x﹣1，x∈N* ， 满足：（i）B={f（x）|x∈A}；（ii）对任意x1 ， x2∈A，当x1＜x2时，恒有f（x1）＜f（x2），所以选项A是“保序同构”；
对于A={x|﹣1≤x≤3}，B={x|x=﹣8或0＜x≤10}，存在函数 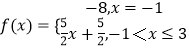，满足：
（i）B={f（x）|x∈A}；（ii）对任意x1 ， x2∈A，当x1＜x2时，恒有f（x1）＜f（x2），所以选项B是“保序同构”；
对于A={x|0＜x＜1}，B=R，存在函数f（x）=tan（ ），满足：（i）B={f（x）|x∈A}；
（ii）对任意
x1 ， x2∈A，当x1＜x2时，恒有f（x1）＜f（x2），所以选项C是“保序同构”；
前三个选项中的集合对是“保序同构”，由排除法可知，不是“保序同构”的只有D．
故选D．
【考点精析】通过灵活运用函数单调性的判断方法，掌握单调性的判定法：①设x1,x2是所研究区间内任两个自变量，且x1＜x2；②判定f(x1)与f(x2)的大小；③作差比较或作商比较即可以解答此题．