题目内容
已知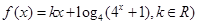 是偶函数.
是偶函数.
(1)求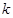 的值;
的值;
(2)证明:对任意实数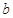 ,函数
,函数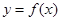 的图像与直线
的图像与直线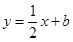 最多只有一个交点;
最多只有一个交点;
(3)设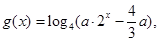 若函数
若函数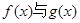 的图像有且只有一个公共点,求实数
的图像有且只有一个公共点,求实数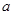 的取值范围.
的取值范围.
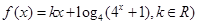 是偶函数.
是偶函数.(1)求
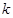 的值;
的值;(2)证明:对任意实数
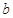 ,函数
,函数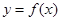 的图像与直线
的图像与直线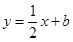 最多只有一个交点;
最多只有一个交点;(3)设
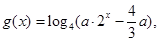 若函数
若函数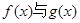 的图像有且只有一个公共点,求实数
的图像有且只有一个公共点,求实数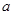 的取值范围.
的取值范围.(1)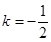 ;(2)证明见解析;(3)
;(2)证明见解析;(3)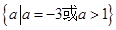 .
.
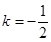 ;(2)证明见解析;(3)
;(2)证明见解析;(3)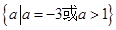 .
.试题分析:(1)由
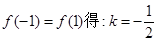 ,并进行检验;(2)原问题等价于证明方程组
,并进行检验;(2)原问题等价于证明方程组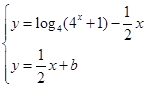 最多只有一组解,即证方程
最多只有一组解,即证方程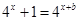 最多只有一个实根,利用反证法证明该方程不可能有两个实根,所以原命题得证;(3)问题转化为方程:
最多只有一个实根,利用反证法证明该方程不可能有两个实根,所以原命题得证;(3)问题转化为方程: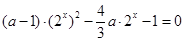 只有唯一解,令
只有唯一解,令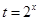 ,则可化为关于
,则可化为关于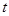 的方程:
的方程: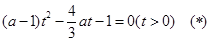 只有唯一正根,注意讨论二次项系数为0和不为0两种情形,当二次项系数不为0时,利用二次函数根的判定方法,最终可以得到所求实数
只有唯一正根,注意讨论二次项系数为0和不为0两种情形,当二次项系数不为0时,利用二次函数根的判定方法,最终可以得到所求实数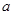 的取值范围.
的取值范围.试题解析:解:(1)由
 经检验的
经检验的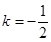 满足题意; 2分
满足题意; 2分(2)证明:即证方程组
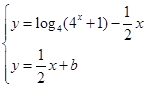 最多只有一组解,
最多只有一组解,即证方程
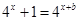 最多只有一个实根. 4分
最多只有一个实根. 4分下面用反证法证明:
假设上述方程有两个不同的解
 则有:
则有: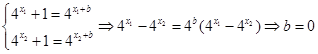 .
.但
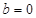 时,
时,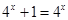 不成立.
不成立.故假设不成立.从而结论成立. 7分
(3)问题转化为方程:
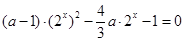 只有唯一解. 9分
只有唯一解. 9分令
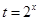 ,则可化为关于
,则可化为关于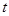 的方程:
的方程: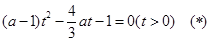 只有唯一正根. 10分
只有唯一正根. 10分若
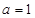 ,则上述方程变为
,则上述方程变为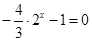 ,无解.故
,无解.故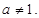 11分
11分若二次方程(*)两根异号,即
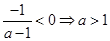 .此时方程(*)有唯一正根,满足条件; 12分
.此时方程(*)有唯一正根,满足条件; 12分若二次方程(*)两根相等且为正,则
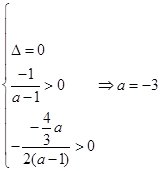 . 13分
. 13分故
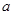 的取值范围是:
的取值范围是: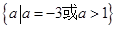 . 14分
. 14分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
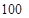 度时,按每度
度时,按每度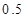 元计费,每月用电超过
元计费,每月用电超过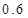 元计费,每月用电超过
元计费,每月用电超过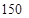 度时,超过部分按每度
度时,超过部分按每度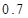 元计费
元计费 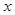 度,应交电费
度,应交电费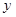 元,写出
元,写出 的定义域为
的定义域为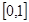 ,且同时满足以下三个条件:①
,且同时满足以下三个条件:① ;②对任意的
;②对任意的 ,都有
,都有 ;③当
;③当 时总有
时总有 .
. 的值;
的值; 时,恒有
时,恒有 .
. 若存在
若存在 ,使得
,使得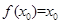 成立,则称
成立,则称 为
为
 时,求函数
时,求函数 的不动点;
的不动点;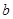 ,函数
,函数 的取值范围;
的取值范围; 图象上
图象上 、
、 两点的横坐标是函数
两点的横坐标是函数 对称,求
对称,求 在区间
在区间 上有最大值4,最小值1,
上有最大值4,最小值1, 的值。
的值。 不等式
不等式 在区间
在区间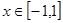 上恒成立,求实数k的取值范围?
上恒成立,求实数k的取值范围?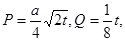 其中
其中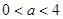 ,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元),
,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元),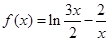 的零点一定位于区间( ).
的零点一定位于区间( ).
 ]
] ]
] ]
] ]
] 的零点所在的一个区间是
的零点所在的一个区间是