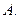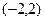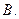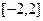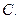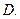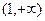题目内容
记函数f(x)=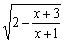 的定义域为A,g(x)=lg[(x-a-1)(2a-x)](a<1)的定义域为B.
的定义域为A,g(x)=lg[(x-a-1)(2a-x)](a<1)的定义域为B.
(1)求A;
(2)若B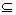 A,求实数a的取值范围.
A,求实数a的取值范围.
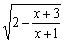 的定义域为A,g(x)=lg[(x-a-1)(2a-x)](a<1)的定义域为B.
的定义域为A,g(x)=lg[(x-a-1)(2a-x)](a<1)的定义域为B.(1)求A;
(2)若B
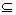 A,求实数a的取值范围.
A,求实数a的取值范围.(1)A=(-∞,-1)∪[1,+∞)
(2) (-∞,-2]∪[
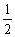 ,1).
,1).(1)由2-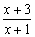 ≥0,得
≥0,得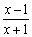 ≥0,
≥0,
∴x<-1或x≥1,即A=(-∞,-1)∪[1,+∞).
(2) 由(x-a-1)(2a-x)>0,得(x―a―1)(x-2a)<0.
∵a<1,∴a+1>2a,∴B=(2a,a+1).
∵B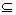 A,∴2a≥1或a+1≤-1,即a≥
A,∴2a≥1或a+1≤-1,即a≥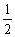 或a≤-2.
或a≤-2.
而a<1,∴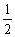 ≤a<1或a≤-2.
≤a<1或a≤-2.
故当B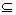 A时,实数a的取值范围是(-∞,-2]∪[
A时,实数a的取值范围是(-∞,-2]∪[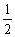 ,1).
,1).
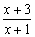 ≥0,得
≥0,得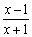 ≥0,
≥0, ∴x<-1或x≥1,即A=(-∞,-1)∪[1,+∞).
(2) 由(x-a-1)(2a-x)>0,得(x―a―1)(x-2a)<0.
∵a<1,∴a+1>2a,∴B=(2a,a+1).
∵B
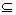 A,∴2a≥1或a+1≤-1,即a≥
A,∴2a≥1或a+1≤-1,即a≥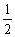 或a≤-2.
或a≤-2.而a<1,∴
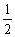 ≤a<1或a≤-2.
≤a<1或a≤-2.故当B
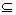 A时,实数a的取值范围是(-∞,-2]∪[
A时,实数a的取值范围是(-∞,-2]∪[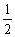 ,1).
,1).
练习册系列答案
相关题目
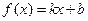 的图象过点
的图象过点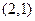 ,且方向向量
,且方向向量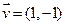 .
.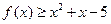 的解集为
的解集为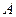 ,且
,且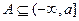 .
.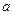 的取值范围; (2)解关于
的取值范围; (2)解关于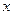 的不等式
的不等式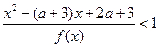 .
. 1) 把总造价
1) 把总造价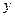 元表示为池底的一边长
元表示为池底的一边长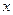 米的函数;
米的函数;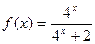 ,那么
,那么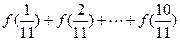 的值为_______
的值为_______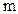 长的直线型通道,中国馆位于世博轴的一侧. 现测得中国馆到世博轴两端的距离相等,并且从中国馆看世博轴两端的视角为
长的直线型通道,中国馆位于世博轴的一侧. 现测得中国馆到世博轴两端的距离相等,并且从中国馆看世博轴两端的视角为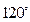 . 据此数据计算,中国馆到世博轴其中一端的距离是
. 据此数据计算,中国馆到世博轴其中一端的距离是  ( )
( ) 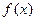 的图像是连续不断的,且
的图像是连续不断的,且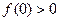 ,
,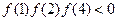 ,则下列命题正确的是( )
,则下列命题正确的是( )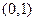 内有零点 B: 函数
内有零点 B: 函数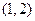 内有零点
内有零点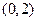 内有零点 D: 函数
内有零点 D: 函数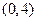 内有零点
内有零点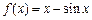 的零点个数为
的零点个数为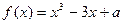 有3个不同的零点,则实数
有3个不同的零点,则实数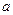 的取值范围是( )
的取值范围是( )