题目内容
(本小题12分)
已知函数
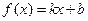 的图象过点
的图象过点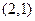 ,且方向向量
,且方向向量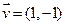 .
.若不等式
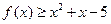 的解集为
的解集为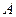 ,且
,且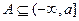 .
.(1)求
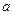 的取值范围; (2)解关于
的取值范围; (2)解关于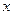 的不等式
的不等式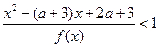 .
.(1)
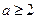
(2)当
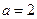 时,不等式的解集为
时,不等式的解集为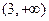 ,
,当
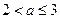 时,不等式的解集为
时,不等式的解集为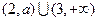 ,
,当
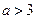 时,不等式的解集为
时,不等式的解集为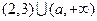
(1)因直线的方向向量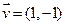 ,∴
,∴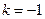 ,由点斜式可得直线:
,由点斜式可得直线:
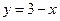 , ∴
, ∴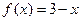 .
.
由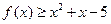 ,得
,得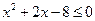 ,∴
,∴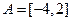 ,
,
又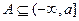 ,∴
,∴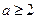 ,
,
故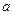 的取值范围是
的取值范围是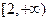 . (6分)
. (6分)
(2)由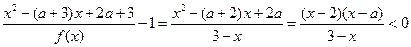 ,
,
得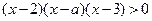 .
.
①当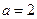 时,
时,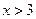 ; ②当
; ②当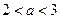 时,
时,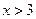 或
或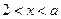 ;
;
③当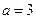 时,
时,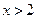 且
且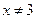 ;④当
;④当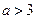 时,
时,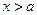 或
或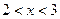 ;
;
综上, 当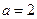 时,不等式的解集为
时,不等式的解集为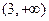 ,
,
当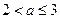 时,不等式的解集为
时,不等式的解集为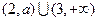 ,
,
当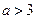 时,不等式的解集为
时,不等式的解集为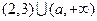 . (12分)
. (12分)
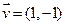 ,∴
,∴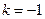 ,由点斜式可得直线:
,由点斜式可得直线: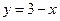 , ∴
, ∴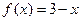 .
.由
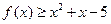 ,得
,得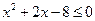 ,∴
,∴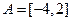 ,
,又
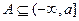 ,∴
,∴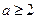 ,
,故
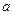 的取值范围是
的取值范围是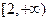 . (6分)
. (6分)(2)由
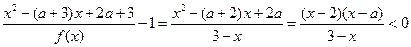 ,
,得
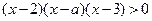 .
.①当
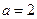 时,
时,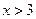 ; ②当
; ②当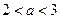 时,
时,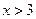 或
或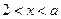 ;
;③当
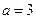 时,
时,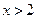 且
且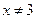 ;④当
;④当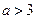 时,
时,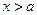 或
或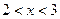 ;
;综上, 当
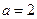 时,不等式的解集为
时,不等式的解集为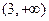 ,
,当
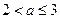 时,不等式的解集为
时,不等式的解集为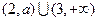 ,
,当
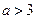 时,不等式的解集为
时,不等式的解集为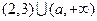 . (12分)
. (12分)
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
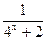 (x∈R),P1(x1,y1),P2(x2,y2)是函数y=f(x)图像上两点,且线段P1P2中点P的横坐标为
(x∈R),P1(x1,y1),P2(x2,y2)是函数y=f(x)图像上两点,且线段P1P2中点P的横坐标为 。
。 }的通项公式为
}的通项公式为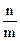 )(m∈N
)(m∈N ,n=1,2,3,…,m),求数列{
,n=1,2,3,…,m),求数列{ ; (5分)
; (5分)
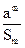 <
< 横成立,求实数a的取值范围。(3分)
横成立,求实数a的取值范围。(3分)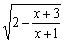 的定义域为A,g(x)=lg[(x-a-1)(2a-x)](a<1)的定义域为B.
的定义域为A,g(x)=lg[(x-a-1)(2a-x)](a<1)的定义域为B.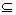 A,求实数a的取值范围.
A,求实数a的取值范围. ,则S的最小值是____ ____
,则S的最小值是____ ____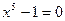 的虚根,可以把原方程变形为
的虚根,可以把原方程变形为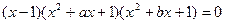 ,
,
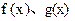 表示同一函数的是( )
表示同一函数的是( )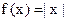 与
与 B
B 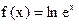 与
与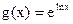
 与
与 D
D  与
与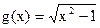
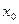 是方程
是方程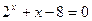 的解,且
的解,且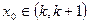 ,
,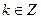 ,则
,则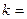 ___________.
___________. 的函数
的函数
 ,若关于
,若关于 的方程
的方程 有三个不同的实数解
有三个不同的实数解 、
、 、
、 ,则
,则 ___________
___________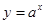 在R内单调递减;
在R内单调递减; 与x轴交于不同的两点。
与x轴交于不同的两点。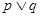 为真,
为真, 也为真,求a的取值范围。
也为真,求a的取值范围。