题目内容
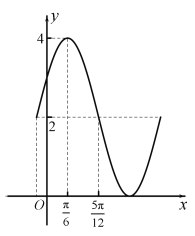
【题目】函数f(x)=Asin(ωx+φ)+B的部分图象如图所示,其中A>0,ω>0,|φ|![]() .
.
(Ⅰ)求函数y=f(x)解析式;
(Ⅱ)求x∈[0,![]() ]时,函数y=f(x)的值域.
]时,函数y=f(x)的值域.
【答案】(Ⅰ)f(x)=2sin(2x![]() )+2;(Ⅱ)[1,4].
)+2;(Ⅱ)[1,4].
【解析】
(Ⅰ)根据已知图象,分析出A,B,T,然后求出ω的值.根据五点作图法求出φ的值.综合即可写出函数f(x)的解析式.
(Ⅱ)由已知可求范围2x![]() ∈[
∈[![]() ,
,![]() ],利用正弦函数的图象和性质可得sin(2x
],利用正弦函数的图象和性质可得sin(2x![]() )∈[
)∈[![]() ,1],即可求解
,1],即可求解
解:(Ⅰ)∵根据函数f(x)=Asin(ωx+)+B的一部分图象,其中A>0,ω>0,|φ|![]() ,可得A=4﹣2=2,B=2,
,可得A=4﹣2=2,B=2,![]() ,
,
∴ω=2,又∵2![]() φ
φ![]() ,∴φ
,∴φ![]() ,
,
∴f(x)=2sin(2x![]() )+2.
)+2.
(Ⅱ)∵x∈[0,![]() ],
],
∴2x![]() ∈[
∈[![]() ,
,![]() ],
],
∴sin(2x![]() )∈[
)∈[![]() ,1],
,1],
∴y=f(x)∈[1,4].

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目