题目内容
直线
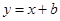 与抛物线
与抛物线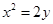 交于A、B两点,O为坐标原点,且
交于A、B两点,O为坐标原点,且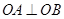 ,则
,则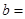 ( )
( )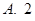
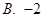
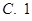
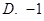
A
分析:先设A(x1,y1)B(x2,y2)联立方程可得
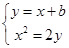 即x2-2x-2b=0有两个不同的解,由OA⊥OB可得x1x2+y1y2=0,代入整理可得关于b的方程,从而可求b的值
即x2-2x-2b=0有两个不同的解,由OA⊥OB可得x1x2+y1y2=0,代入整理可得关于b的方程,从而可求b的值解:设A(x1,y1)B(x2,y2)
联立方程可得
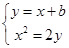
即x2-2x-2b=0有两个不同于原点的解
∴x1+x2=2,x1x2=-2b,△=4+8b>0
∵OA⊥OB?
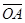 ?
?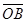 =0
=0∴x1x2+y1y2=0?x1x2+(x1+b)(x2+b)=0
整理可得2x1x2+b(x1+x2)+b2=0
∴b2-2b=0
∴b=0(舍)或b=2
故答案为:2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

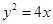 的焦点坐标为 ( ■ )
的焦点坐标为 ( ■ )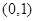
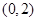
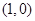
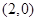
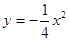 的焦点坐标是:
的焦点坐标是: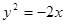
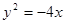
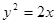
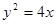
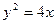 的焦点是F,点P是抛物线上的动点,又有点A(3,2),求
的焦点是F,点P是抛物线上的动点,又有点A(3,2),求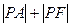 最小值,并求此时P点的坐标.
最小值,并求此时P点的坐标.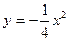 上的动点
上的动点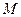 到两定点(0,-1)、(1,-3)的距离之和的最小值为______________________
到两定点(0,-1)、(1,-3)的距离之和的最小值为______________________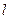 时,拱顶离水面2米,水面宽4米,(1)建立如下图所示的直角坐标系,求抛物线的解析式。(2)水面下降1米后,水面宽是多少?
时,拱顶离水面2米,水面宽4米,(1)建立如下图所示的直角坐标系,求抛物线的解析式。(2)水面下降1米后,水面宽是多少?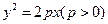 ,过定点
,过定点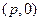 作两条互相垂直的直线
作两条互相垂直的直线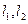 ,若
,若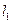 与抛物线交于点
与抛物线交于点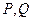 ,
,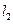 与抛物线交于
与抛物线交于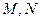 点,
点,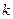 .某同学已正确求得弦
.某同学已正确求得弦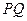 的中点坐标为
的中点坐标为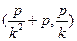 ,请写出弦
,请写出弦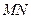 的中点坐标 .
的中点坐标 .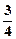 m,则水面上涨到与抛物线拱顶相距
m,则水面上涨到与抛物线拱顶相距