题目内容
盒中有6只灯泡,其中2只次品,4只正品,有放回地从中任取两次,每次取一只,试求下列事件的概率:(1)取到的2只都是次品;(2)取到的2只中正品、次品各一只;
(3)取到的2只中至少有一只正品.
(3)取到的2只中至少有一只正品.
(Ⅰ)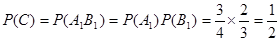 .
.
(Ⅱ)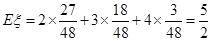 .
.
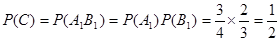 .
. (Ⅱ)
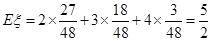 .
. (I)设该人参加科目A考试合格和补考为时间A1、A2,参加科目B考试合格和补考合格为时间B1、B2,事件A1、A2、B1、B2互为独立,设该人不需要补考就可以获得证书为事件C,则C=A1B1,然后根据相互独立事件的概率乘法公式可求出所求;
(II)ζ的取值可能为2,3,4,然后根据相互独立事件的概率乘法公式分别求出相应的概率,最后根据离散型随机变量的数学期望公式解之即可.
设该人参加科目A考试合格和补考为时间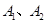 ,参加科目B考试合格和补考合格为时间
,参加科目B考试合格和补考合格为时间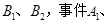
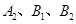 相互独立.
相互独立.
(Ⅰ)设该人不需要补考就可获得证书为事件C,则C=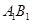 ,
,
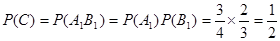 . …………………4分
. …………………4分
(Ⅱ)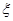 的可能取值为2,3,4. 则
的可能取值为2,3,4. 则
P(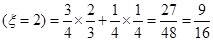 ;
;
P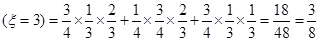 ;
;
P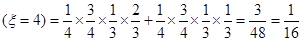 . …………………9分
. …………………9分
所以,随即变量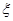 的分布列为
的分布列为
所以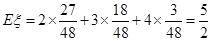 . ………………12分
. ………………12分
(II)ζ的取值可能为2,3,4,然后根据相互独立事件的概率乘法公式分别求出相应的概率,最后根据离散型随机变量的数学期望公式解之即可.
设该人参加科目A考试合格和补考为时间
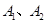 ,参加科目B考试合格和补考合格为时间
,参加科目B考试合格和补考合格为时间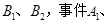
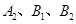 相互独立.
相互独立.(Ⅰ)设该人不需要补考就可获得证书为事件C,则C=
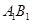 ,
,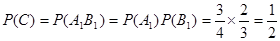 . …………………4分
. …………………4分(Ⅱ)
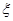 的可能取值为2,3,4. 则
的可能取值为2,3,4. 则P(
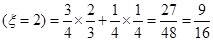 ;
;P
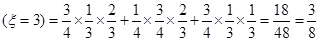 ;
;P
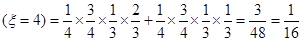 . …………………9分
. …………………9分所以,随即变量
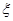 的分布列为
的分布列为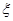 | 2 | 3 | 4 |
| P | 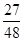 | 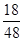 | 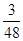 |
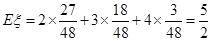 . ………………12分
. ………………12分
练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 、
、 、
、 。指标甲、乙、丙合格分别记为4分、2分、4分;若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。
。指标甲、乙、丙合格分别记为4分、2分、4分;若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。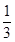 ,将赝品错误地鉴定为正品的概率为
,将赝品错误地鉴定为正品的概率为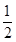 ,已知一批物品共有4件,其中正品3件,赝品1件.(1)求该收藏爱好者的鉴定结果为正品2件,赝品2件的概率;(2)求该收藏爱好者的鉴定结果中正品数
,已知一批物品共有4件,其中正品3件,赝品1件.(1)求该收藏爱好者的鉴定结果为正品2件,赝品2件的概率;(2)求该收藏爱好者的鉴定结果中正品数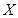 的分布列及数学期望.
的分布列及数学期望. 为选出的4个人中选科目甲的人数,求
为选出的4个人中选科目甲的人数,求 (
( )个大小相同的球,其中有3个红球和
)个大小相同的球,其中有3个红球和 个白球.已知从
个白球.已知从 ,且
,且 。若有放回地从口袋中连续地取四次球(每次只取一个球),在四次取球中恰好取到两次红球的概率大于
。若有放回地从口袋中连续地取四次球(每次只取一个球),在四次取球中恰好取到两次红球的概率大于 。
。 为第一次取到白球时的取球次数,求
为第一次取到白球时的取球次数,求 。
。 是一个离散型随机变量,其分布列如下表,试求随机变量
是一个离散型随机变量,其分布列如下表,试求随机变量 与方差
与方差 .
.
 ,求
,求 ,则
,则 ( )
( )


