题目内容
【题目】椭圆C焦点在y轴上,离心率为 ![]() ,上焦点到上顶点距离为2﹣
,上焦点到上顶点距离为2﹣ ![]() .
.
(1)求椭圆C的标准方程;
(2)直线l与椭圆C交与P,Q两点,O为坐标原点,△OPQ的面积S△OPQ=1,则| ![]() |2+|
|2+| ![]() |2是否为定值,若是求出定值;若不是,说明理由.
|2是否为定值,若是求出定值;若不是,说明理由.
【答案】
(1)解:由题意可得  ,
,
解得 ![]() ,
,
可得b2=a2﹣c2=1,
即有椭圆C的标准方程为: ![]() ;
;
(2)解:设P(x1,y1),Q(x2,y2)
①当l斜率不存在时,P,Q两点关于x轴对称,
S△OPQ=|x1||y1|=1,
又 ![]() ,解得
,解得 ![]() ,
,
| ![]() |2+|
|2+| ![]() |2=2(x12+y12)=2×(
|2=2(x12+y12)=2×( ![]() +2)=5;
+2)=5;
②当直线l的斜率存在时,设直线l的方程为y=kx+m,
由题意知m≠0,将其代入 ![]() ,得
,得
(k2+4)x2+2kmx+m2﹣4=0,
即有 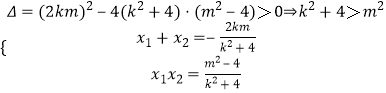 ,
,
则 ![]() ,O到PQ距离
,O到PQ距离 ![]() ,
,
则 ![]() ,
,
解得k2+4=2m2,满足△>0,
则 ![]() ,
,
即有| ![]() |2+|
|2+| ![]() |2=(x12+y12)(x22+y22)
|2=(x12+y12)(x22+y22)
= ![]()
= ![]() =﹣3+8=5,
=﹣3+8=5,
综上可得| ![]() |2+|
|2+| ![]() |2为定值5.
|2为定值5.
【解析】(1)运用椭圆的离心率公式和两点的距离公式,及a,b,c的关系,解得a,b,进而得到椭圆方程;(2)设P(x1 , y1),Q(x2 , y2),讨论直线l的斜率不存在和存在,设出直线方程,代入椭圆方程,运用韦达定理和判别式大于0,结合三角形的面积公式,点到直线的距离公式和弦长公式,化简整理,即可得到所求和为定值5.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目