题目内容
已知函数f(x)=
(ax-a-x),其中a>0,a≠1
(1)写出f(x)的奇偶性与单调性(不要求证明);
(2)若函数y=f(x)的定义域为(-1,1),求满足不等式f(m2-1)+f(m-1)<0的实数m的取值集合;
(3)当a∈(-∞,2)时,f(x)-4的值恒为负,求a的取值范围.
| a |
| a2-1 |
(1)写出f(x)的奇偶性与单调性(不要求证明);
(2)若函数y=f(x)的定义域为(-1,1),求满足不等式f(m2-1)+f(m-1)<0的实数m的取值集合;
(3)当a∈(-∞,2)时,f(x)-4的值恒为负,求a的取值范围.
考点:数列与函数的综合
专题:函数的性质及应用,不等式的解法及应用
分析:(1)运用f(-x)与f(x)关系式判断奇偶性,结合指数函数的单调性判断f(x)的单调性,
(2)根据单调性,奇偶性转化为-1<1-m<m2-1<1,求解.
(3)根据单调性得出f(2)-4≤0,即
(a2-a-2)-4=
-4≤0,求解即可.
(2)根据单调性,奇偶性转化为-1<1-m<m2-1<1,求解.
(3)根据单调性得出f(2)-4≤0,即
| a |
| a2-1 |
| a2+1 |
| a |
解答:
解:(1)∵函数f(x)=
(ax-a-x),其中a>0,a≠1,
∴f(-x)=
(a-x-ax)=-f(x),其中a>0,a≠1
∴f(x)是R上的奇函数,且在R上单调递增
(2)由f(x)的奇偶性可得f(1-m)<f(m2-1)
由f(x)的定义域及单调性可得-1<1-m<m2-1<1,
解不等式组可得 1<m<
(3)由于f(x)在(-∞,2)上单调递增,要f(x)-4恒负,
只需f(2)-4≤0,
即
(a2-a-2)-4=
-4≤0,
2-
≤a≤2+
,
结合a>0且a≠1可得:2-
≤a≤2+
且a≠1,
| a |
| a2-1 |
∴f(-x)=
| a |
| a2-1 |
∴f(x)是R上的奇函数,且在R上单调递增
(2)由f(x)的奇偶性可得f(1-m)<f(m2-1)
由f(x)的定义域及单调性可得-1<1-m<m2-1<1,
解不等式组可得 1<m<
| 2 |
(3)由于f(x)在(-∞,2)上单调递增,要f(x)-4恒负,
只需f(2)-4≤0,
即
| a |
| a2-1 |
| a2+1 |
| a |
2-
| 3 |
| 3 |
结合a>0且a≠1可得:2-
| 3 |
| 3 |
点评:本题考察了有关的指数函数的单调性,奇偶性,运用求解不等式式的解集,属于中档题.

练习册系列答案
相关题目
已知a=log
3,b=log
2,c=20.3,则a,b,c三者的大小关系是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、c>b>a |
| B、a>c>b |
| C、b>a>c |
| D、c>a>b |
已知在正四面体ABCD中,E、F分别是线段AB和线段CD上一点,且AE=
AB,CF=
CD,则直线DE和BF所成角的余弦值是( )
| 1 |
| 4 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
下列结论正确的是( )
| A、在同一直角坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点 | ||||||||||||
B、已知向量
| ||||||||||||
| C、在△ABC中,A>B的充要条件是sinA>sinB | ||||||||||||
D、从总体中随机抽出一个容量为20的样本,其数据的分组及各组的频数如下表,则估计总体的中位数为18
|
设a<-1,则关于x的不等式a(x-a)(x-
)<0的解集是( )
| 1 |
| a |
A、{x|x<a或>
| ||
| B、{x|x>a} | ||
C、{x|x>a或x<
| ||
D、{x|x<
|
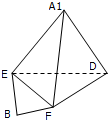 如图,边长为2的正方形ABCD中,E是AB边上的点,F是边BC上的点,且BE=BF,若将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A1.
如图,边长为2的正方形ABCD中,E是AB边上的点,F是边BC上的点,且BE=BF,若将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A1.