题目内容
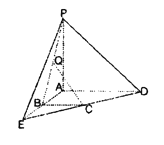
【题目】在六条棱长分别为2、3、3、4、5、5的所有四面体中,最大的体积是多少?证明你的结论.
【答案】![]() ;证明见解析
;证明见解析
【解析】
根据三角形两边之差小于第三边这个性质,按题设数据,所有一边是2的三角形其余两边只可能是(A)3,3;(B)5,5;(C)4,5;(D)3,4,从而题设四面体中,以棱长为2的棱为公共边的两个面的其余两边只可能是下列三种情形:(I)(A)与(B),(II)(A)与(C);(III)(B)与(C),于是问题转化为对棱长分别为(I)(II)(III)的四面体来计算体积的最大值(或估计).
由三角形两边之差小于第三边这个性质,按题设数据,所有一边是2的三角形其余两边只可能是(A)3,3;(B)5,5;(C)4,5;(D)3,4,从而题设四面体中,以棱长为2为公共边的两个面的其余两边只可能是下列三种情形:(I)(A)与(B),(II)(A)与(C);(III)(B)与(C).
对情形(I)(A)与(B),四边形![]() 沿
沿![]() AB折叠后使
AB折叠后使![]() ,则由
,则由![]() 得
得![]() ,即
,即![]() 是四面体以
是四面体以![]() 为底面的高,
为底面的高,
∴体积为![]() ;
;

对情形(II)(A)与(C)四边形![]() 沿
沿![]() AB折叠后使
AB折叠后使![]() ,有两种情形,它们体积相等,记为
,有两种情形,它们体积相等,记为![]() ,∵
,∵![]() ,∴
,∴![]() 为钝角,
为钝角,![]() 与平面
与平面![]() 斜交,
斜交,
∴![]() ;
;

对情形(III),(B)与(C),这样的四面体也有两个,体积也相等,记为![]() ,
,
![]() .
.

∴最大体积为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目