题目内容
14．AD、BE分别为△ABC的边BC、AC上的中线，且$\overrightarrow{AD}$=$\overrightarrow{a}$，$\overrightarrow{BE}$=$\overrightarrow{b}$，那么$\overrightarrow{BC}$为（ ）| A． | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{4}{3}$$\overrightarrow{b}$ | B． | $\frac{2}{3}$$\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$ | C． | $\frac{2}{3}$$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$ | D． | -$\frac{2}{3}$$\overrightarrow{a}$+$\frac{4}{3}$$\overrightarrow{b}$ |
分析 如图所示，$\overrightarrow{BC}=\overrightarrow{BE}+\overrightarrow{EC}$，$\overrightarrow{EC}$=$\frac{1}{2}\overrightarrow{AC}$，$\overrightarrow{AC}$=$\overrightarrow{AD}+\overrightarrow{DC}$，$\overrightarrow{DC}=\frac{1}{2}\overrightarrow{BC}$，即可得出．
解答 解：如图所示，
$\overrightarrow{BC}=\overrightarrow{BE}+\overrightarrow{EC}$，$\overrightarrow{EC}$=$\frac{1}{2}\overrightarrow{AC}$，$\overrightarrow{AC}$=$\overrightarrow{AD}+\overrightarrow{DC}$，$\overrightarrow{DC}=\frac{1}{2}\overrightarrow{BC}$，
∴$\overrightarrow{BC}$=$\overrightarrow{BE}$+$\frac{1}{2}（\overrightarrow{AD}+\frac{1}{2}\overrightarrow{BC}）$，
化为$\overrightarrow{BC}$=$\frac{2}{3}\overrightarrow{a}$+$\frac{4}{3}\overrightarrow{b}$．
故选：A．
点评 本题考查了向量的三角形法则、向量共线定理、平面向量基本定理，考查了推理能力与计算能力，属于中档题．
| A． |  | B． |  | C． |  | D． |  |
| A． | $\frac{8\sqrt{15}}{5}$ | B． | $\sqrt{15}$ | C． | $\frac{\sqrt{15}}{2}$ | D． | 6$\sqrt{3}$ |
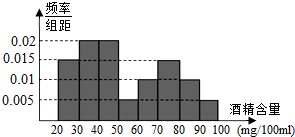据《南通日报》报道，2015年1月1日至1月31日，市交管部门共抽查了1000辆车，查出酒后驾车和醉酒驾车的驾驶员80人，如图是对这80人血液中酒精含量进行检查所得结果的频率分布直方图．（酒精含量≥80mg/100ml为醉酒驾车）（1）根据频率分布直方图完成下表：
| 酒精含量（单位：mg/100ml） | [20，30） | [30，40） | [40，50） | [50，60） |
| 人数 | 16 | 16 | 4 | |
| 酒精含量（单位：mg/100ml） | [60，70） | [70，80） | [80，90） | [90，100] |
| 人数 | 4 |
（3）若用分层抽样的方法从血液酒精浓度在[70，90）范围内的驾驶员中抽取一个容量为5的样本，并将该样本看成一个总体，从中任取2人，求恰有1人属于醉酒驾车的概率．