题目内容
已知集合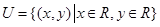 ,
,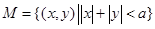 ,
,
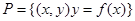 ,现给出下列函数:①
,现给出下列函数:①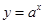 ②
②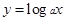 ③
③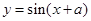 ④
④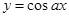 ,若
,若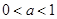 时,恒有
时,恒有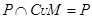 ,则
,则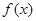 所有可取的函数的编号是( )
所有可取的函数的编号是( )
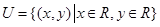 ,
,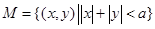 ,
,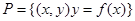 ,现给出下列函数:①
,现给出下列函数:①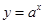 ②
②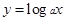 ③
③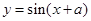 ④
④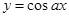 ,若
,若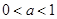 时,恒有
时,恒有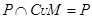 ,则
,则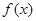 所有可取的函数的编号是( )
所有可取的函数的编号是( )| A.①②③④ | B.①②④ | C.①② | D.④ |
C
答案应选B
利用补集的定义求出?uM,由P∩?uM=P,得到P??uM,故P中的函数f(x)必须满足||x|+|y|≥a,检验各个选项是否满足此条件.
解答:解:∵?uM={(x,y)||x|+|y|≥a},0<a<1时,P∩?uM=P,∴P={(x,y)y=f(x)}??uM,
如图所示:
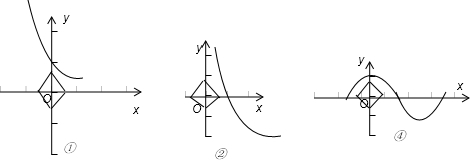
结合图形可得满足条件的函数图象应位于曲线|x|+|y|=a(-a≤x≤a )的上方.
①中,x∈R,y>0,满足|x|+|y|≥a,故①可取.
②中,x>0,y=logax∈R,满足||x|+|y|≥a,故②可取.
③中的函数不满足条件,如 x=0,a=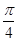 时,y=
时,y=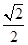 ,不满足|x|+|y|≥a.
,不满足|x|+|y|≥a.
④中x∈R,-1≤y≤1,满足||x|+|y|≥a,故④可取.
故选B.
利用补集的定义求出?uM,由P∩?uM=P,得到P??uM,故P中的函数f(x)必须满足||x|+|y|≥a,检验各个选项是否满足此条件.
解答:解:∵?uM={(x,y)||x|+|y|≥a},0<a<1时,P∩?uM=P,∴P={(x,y)y=f(x)}??uM,
如图所示:
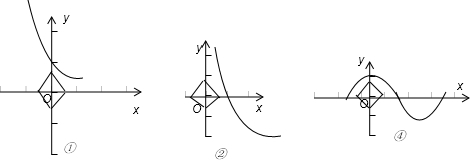
结合图形可得满足条件的函数图象应位于曲线|x|+|y|=a(-a≤x≤a )的上方.
①中,x∈R,y>0,满足|x|+|y|≥a,故①可取.
②中,x>0,y=logax∈R,满足||x|+|y|≥a,故②可取.
③中的函数不满足条件,如 x=0,a=
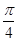 时,y=
时,y=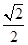 ,不满足|x|+|y|≥a.
,不满足|x|+|y|≥a.④中x∈R,-1≤y≤1,满足||x|+|y|≥a,故④可取.
故选B.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
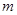 、
、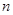 与平面
与平面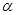 、
、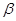 ,有下列四个命题:
,有下列四个命题: 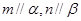 且
且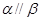 ,则
,则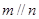 ;
; 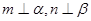 且
且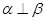 ,则
,则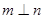 ;
;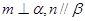 且
且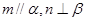 且
且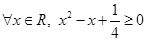 ,则命题p的否定
,则命题p的否定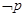 是 ( )
是 ( )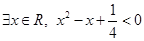
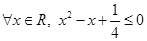

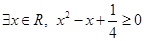
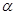 ⊥平面
⊥平面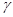 ,平面
,平面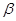 ⊥平面
⊥平面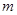 ∥平面
∥平面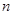 ∥平面
∥平面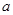 ⊥平面
⊥平面 和平面
和平面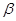 ,则下列推论中正确的是
,则下列推论中正确的是 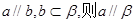
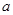 ,
,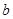 与
与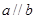
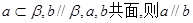
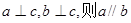
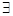 X∈R,lgX=0 B
X∈R,lgX=0 B 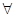 X∈R,X3﹥0 D
X∈R,X3﹥0 D 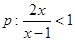 ,
,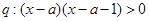 ,若
,若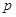 是
是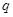 的充分不必要条件,则实数
的充分不必要条件,则实数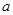 的取值范围是
的取值范围是 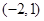
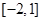
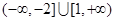
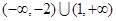 .
.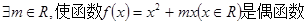
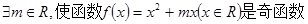
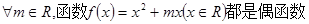
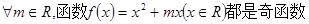
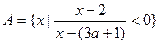 ,
,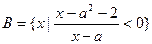 .
.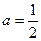 时,求(∁U
时,求(∁U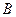 )
)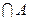 ;
;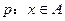 ,命题
,命题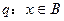 ,若
,若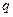 是
是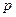 的必要条件,求实数
的必要条件,求实数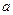 的取值范围
的取值范围