题目内容
13．已知角α的终边经过点A（-$\sqrt{3}$，a），若点A在抛物线y=-$\frac{1}{4}$x2的准线上，则sinα=（ ）| A． | -$\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | -$\frac{1}{2}$ | D． | $\frac{1}{2}$ |
分析 求出抛物线的准线方程，可得a=1，再由任意角的三角函数的定义，即可求得sinα．
解答 解：抛物线y=-$\frac{1}{4}$x2即x2=-4y的准线为y=1，
即有a=1，点A（-$\sqrt{3}$，1），
由任意角的三角函数的定义，可得sinα=$\frac{y}{r}$=$\frac{1}{\sqrt{3+1}}$=$\frac{1}{2}$．
故选D．
点评 本题考查抛物线的方程和性质，主要考查准线方程及运用，同时考查任意角的三角函数的定义，属于基础题．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
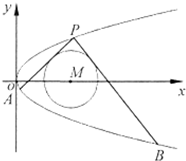已知曲线C：y2=2px（p＞0）过定点（1，1），点P是曲线C上的动点，过点P的圆M：（x-t）2+y2=1（t＞1）的切线l1，l2分别交曲线C于另外两点A，B．