题目内容
16．过抛物线y2=8x焦点F的直线交抛物线于A（x1，y1），B（x2，y2）两点，若x1+x2=5，则|AB|=（ ）| A． | 6 | B． | 7 | C． | 8 | D． | 9 |
分析 根据抛物线的方程求出准线方程是x=-2，结合抛物线的定义可得|AF|=x1+2且|BF|=x2+2，两式相加并结合x1+x2=5，即可得到|AB|的值为9．
解答 解：∵抛物线方程为y2=8x，
∴p=4，可得抛物线的准线方程是x=-2，
∵过抛物线 y2=8x的焦点F作直线交抛物线于A（x1，y1）B（x2，y2），
∴根据抛物线的定义，可得|AF|=x1+$\frac{p}{2}$=x1+2，|BF|=x2+$\frac{p}{2}$=x2+2，
因此，线段AB的长|AB|=|AF|+|BF|=x1+x2+4，
又∵x1+x2=5，∴|AB|=x1+x2+4=9．
故选D．
点评 本题给出抛物线焦点弦AB端点A、B的横坐标的关系式，求AB的长度，着重考查了抛物线的定义、标准方程和简单几何性质等知识，属于中档题．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
4．i是虚数单位，$\overrightarrow{z}$表示复数z的共轭复数，若$\overrightarrow{z}=1+i$，则$\frac{\overrightarrow{z}}{i}+i•z$=（ ）
| A． | -2 | B． | 2 | C． | -2i | D． | 2i |
7．
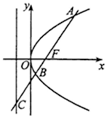如图，过抛物线y2=2px（p＞0）焦点F的直线l交抛物线于点A、B，交其准线于点C，若|BC|=2|BF|，且|AF|=3，则此抛物线的方程为（ ）
如图，过抛物线y2=2px（p＞0）焦点F的直线l交抛物线于点A、B，交其准线于点C，若|BC|=2|BF|，且|AF|=3，则此抛物线的方程为（ ）| A． | y2=3x | B． | y2=9x | C． | y2=$\frac{3}{2}$x | D． | y2=$\frac{9}{2}$x |
11．抛物线x2=6y的准线方程为（ ）
| A． | x=-$\frac{3}{2}$ | B． | x=-3 | C． | y=-$\frac{3}{2}$ | D． | y=-3 |
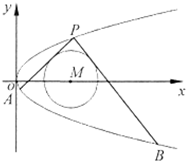已知曲线C：y2=2px（p＞0）过定点（1，1），点P是曲线C上的动点，过点P的圆M：（x-t）2+y2=1（t＞1）的切线l1，l2分别交曲线C于另外两点A，B．