题目内容
3.已知△ABC中B=60°,且边a=4,c=3,则边b=$\sqrt{13}$;△ABC的面积等于3$\sqrt{3}$.分析 由余弦定理进行求解即可.
解答 解:∵B=60°,且边a=4,c=3,
∴b2=a2+c2-2accosB=16+9-2×$4×3×\frac{1}{2}$=13,
则b=$\sqrt{13}$,
则△ABC的面积S=$\frac{1}{2}acsinB$=$\frac{1}{2}×4×3×\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
故答案为:$\sqrt{13},3\sqrt{3}$
点评 本题主要考查余弦定理的应用,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.在复平面内,复数$\frac{{i}^{2015}}{1+i}$对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.否定“自然数a,b,c中至少有一个是偶数”时,正确的反设是( )
| A. | a,b,c都是偶数 | B. | a,b,c至多有一个是偶数 | ||
| C. | a,b,c至少有一个是奇数 | D. | a,b,c都是奇数 |
11.如图所示的程序框图中,若x=5,则输出i的值是( )
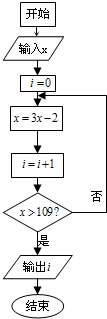

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
8.在△ABC中,$c=\sqrt{2}$,acosC=csinA,若当a=x0时的△ABC有两解,则x0的取值范围是( )
| A. | $(1,\sqrt{2})$ | B. | $(1,\sqrt{3})$ | C. | $(\sqrt{3},2)$ | D. | $(\sqrt{2},2)$ |
15.在△ABC中,若c2+ab=a2+b2,则角C=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
12.执行如图的程序框图,若输入m的值为2,则输出的结果i=( )
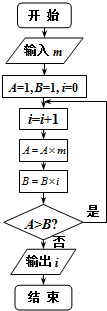

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
13.散点图在回归分析过程中的作用是( )
| A. | 查找个体个数 | B. | 粗略判断变量是否线性相关 | ||
| C. | 探究个体分类 | D. | 比较个体数据大小关系 |