题目内容
(13分)如图(3):四面体D—ABC中,DB⊥面ABC, ∠DAB="30°,∠BAC=45°," ∠ACB=90°.BC=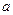 .
.
(1)点A与面BCD的距离; (2)AB与CD成的角的余弦值.
 .
.(1)点A与面BCD的距离; (2)AB与CD成的角的余弦值.
(1) AC=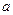 (2)
(2) 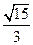
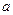 (2)
(2) 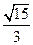
(1)∵DB⊥面ABC ∴DB⊥AC,又BC⊥AC ∴AC⊥面DBC ∴A到面DBC的距离为AC,由题设可得:AC=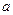
(2)过C作CM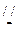 AB.则∠DCM或补角为所求,在△DCM中
AB.则∠DCM或补角为所求,在△DCM中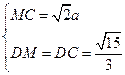
(2)过C作CM
 AB.则∠DCM或补角为所求,在△DCM中
AB.则∠DCM或补角为所求,在△DCM中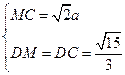

练习册系列答案
相关题目
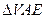 的面积是
的面积是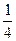 ,则侧棱VA与底面所成角的大小是__________________(结果用反三角函数值表示)。
,则侧棱VA与底面所成角的大小是__________________(结果用反三角函数值表示)。 的一条斜线,点A是平面
的一条斜线,点A是平面 是经过点A的一条动直线,那么下列情形中可能出现的是 ( )
是经过点A的一条动直线,那么下列情形中可能出现的是 ( )



 X∥Y”为真命题的是_________(填序号)
X∥Y”为真命题的是_________(填序号)
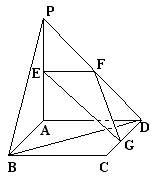
 中,PA=AB=AE=2
中,PA=AB=AE=2 ,PB=PE=
,PB=PE= , BC=DE=
, BC=DE=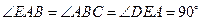 .(Ⅰ)求证:PA
.(Ⅰ)求证:PA 平面
平面 (Ⅱ)求二面角
(Ⅱ)求二面角 的大小。
的大小。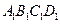 的棱长为l,点F、H分别为为
的棱长为l,点F、H分别为为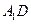 、A1C的中点.
、A1C的中点.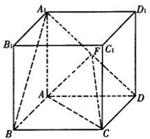
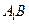 ∥平面AFC;.
∥平面AFC;.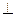 平面AFC.
平面AFC. a.
a.



