题目内容
18.解下列不等式(组):(1)1≤|2x-1|≤3.
(2)$\left\{\begin{array}{l}{{x}^{2}-x-12≤0}\\{\frac{x+2}{x-1}<0}\end{array}\right.$.
分析 (1)去掉绝对值,解不等式取并集即可;(2)通过讨论x的范围,因式分解取交集即可.
解答 解:(1)1≤|2x-1|≤3,
∴-3≤2x-1≤-1或1≤2x-1≤3,
解得:-1≤x≤0或1≤x≤2,
∴原不等式的解集是[-1,0]∪[1,2].
(2)原不等式组等价于:
$\left\{\begin{array}{l}{(x-4)(x+3)≤0}\\{(x+2)(x-1)<0}\end{array}\right.$⇒$\left\{\begin{array}{l}{-3≤x≤4}\\{-2<x<1}\end{array}\right.$,⇒-2<x<1,
∴原不等式组的解集是{x|-2<x<1}.
点评 本题考查了不等式组的解法,考查去绝对值问题,是一道基础题.

练习册系列答案
 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
8.进入高三,为加强营养,某同学每天早餐有四种互不相同套餐可供选择,每天使用其中的一种套餐,且每天都是从头一天中未使用的三种套餐中等可能地随机选用一种.在一周内,现已知他星期一使用A种套餐,那么星期六他也使用A种套餐的概率是( )
| A. | $\frac{58}{243}$ | B. | $\frac{37}{102}$ | C. | $\frac{7}{27}$ | D. | $\frac{20}{81}$ |
3.要得到y=tan(2x-$\frac{π}{3}$)的图象,只要将y=tan2x的图象( )
| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
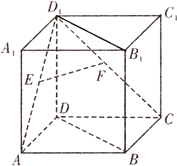 如图,在正方体ABCD-A1B1C1D1中,E、F分别为AD1,CD1中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别为AD1,CD1中点.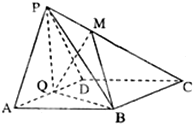 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,且Q为AD的中点.PA=PD=AD=2.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,且Q为AD的中点.PA=PD=AD=2.