题目内容
9. 如图,在正方体ABCD-A1B1C1D1中,E、F分别为AD1,CD1中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别为AD1,CD1中点.(1)求异面直线EF与CD所成角的大小;
(2)求证:EF⊥平面BDD1B1.
分析 (1)连接AC,由EF∥AC,得∠ACD是异面直线EF与CD所成的角,求出这个角的大小即可;
(2)先证明AC⊥平面BDD1B1,再由EF∥AC证明EF⊥平面BDD1B1.
解答 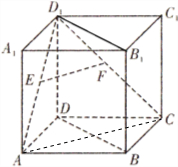 解:(1)如图所示,连接AC,
解:(1)如图所示,连接AC,
∵E、F是AD1,CD1中点,
∴EF∥AC,
∴∠ACD是异面直线EF与CD所成的角,
又∵四边形ABCD是正方形,
∴∠ACD=45°;
即EF与CD所成的角是45°;
(2)证明:正方体ABCD-A1B1C1D1中,四边形ABCD是正方形,
∴AC⊥BD;
又BB1⊥底面ABCD,
AC?平面ABCD,
∴BB1⊥AC,
且BD∩BB1=B,
BD?平面BDD1B1,
BB1?平面BDD1B1,
∴AC⊥平面BDD1B1;
由(1)知,EF∥AC,
∴EF⊥平面BDD1B1.
点评 本题考查了求异面直线所成角的问题,也考查了空间中的平行与垂直关系的应用问题,是基础题目.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
20.已知a<0,-1<b<0,则a,ab,ab2的大小关系式( )
| A. | a>ab>ab2 | B. | ab2>ab>a | C. | ab>a>ab2 | D. | ab>ab2>a |
17.正四棱锥(底面是正方形,顶点在底面的射影落在底面中心的四棱锥)P-ABCD底面的四个顶点A,B,C,D在球O的同一个大圆上,点P在球面上,如果球O的表面积是4π,则四棱锥P-ABCD的体积为( )
| A. | $\frac{16}{3}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | $\frac{4}{3}$ |
4.已知圆的参数方程为$\left\{\begin{array}{l}x=2+\sqrt{2}cosθ\\ y=1+\sqrt{2}sinθ\end{array}\right.(θ为参数)$,那么该圆的普通方程是( )
| A. | ${(x-2)^2}+{(y-1)^2}=\sqrt{2}$ | B. | ${(x+2)^2}+{(y+1)^2}=\sqrt{2}$ | C. | (x-2)2+(y-1)2=2 | D. | (x+2)2+(y+1)2=2 |
14.观察两个变量(存在线性相关关系)得如下数据:
则两变量间的线性回归方程为( )
| x | -10 | -6.99 | -5.01 | -2.98 | 3.98 | 5 | 7.99 | 8.01 |
| y | -9 | -7 | -5 | -3 | 4.01 | 4.99 | 7 | 8 |
| A. | $\hat y$=$\frac{1}{2}$x+1 | B. | $\hat y$=x | C. | $\hat y$=2x+$\frac{1}{3}$ | D. | $\hat y$=x+1 |
19.若(2x-1)2013=a0+a1x+a2x2+…+a2013x2013(x∈R),则$\frac{1}{2}$+$\frac{{a}_{2}}{{2}^{2}{a}_{1}}$+$\frac{{a}_{3}}{{2}^{3}{a}_{1}}$+…+$\frac{{a}_{2013}}{{2}^{2013}{a}_{1}}$=( )
| A. | -$\frac{1}{2013}$ | B. | $\frac{1}{2013}$ | C. | -$\frac{1}{4026}$ | D. | $\frac{1}{4026}$ |
 如图,AB是⊙O的直径,点C是⊙O上的动点,PA垂直于⊙O所在的平面.
如图,AB是⊙O的直径,点C是⊙O上的动点,PA垂直于⊙O所在的平面. 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,∠ACB=90°,2AC=AA1,D,M分别是棱AA1,BC的中点.证明:
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,∠ACB=90°,2AC=AA1,D,M分别是棱AA1,BC的中点.证明: