题目内容
19．
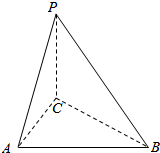如图所示，三棱锥P-ABC中，平面PAB⊥底面ABC，且PA=PB=PC，则△ABC是直角三角形．
分析 设P在平面ABC上的射影为O，确定O是△ABC的外心，且是AB的中点，O∈AB，即可得出结论．
解答 解：设P在平面ABC上的射影为O，则
∵PA=PB=PC，
∴O是△ABC的外心，且是AB的中点，
∵平面PAB⊥底面ABC，
∴O∈AB，
∴△ABC是直角三角形，
故答案为：直角．
点评 本题考查平面与平面垂直的性质，考查直角三角形外心的性质，比较基础．
练习册系列答案
世纪百通期末金卷系列答案
相关题目