题目内容
7.求证:1+$\frac{1}{\sqrt{2}}$+$\frac{1}{\sqrt{3}}$+…+$\frac{1}{\sqrt{n}}$>2($\sqrt{n+1}$-1).分析 不等式右边有个2,所以将不等式左边提取2变成:2($\frac{1}{2}$+$\frac{1}{2\sqrt{2}}$+…+$\frac{1}{2\sqrt{n}}$)>2($\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+…+$\frac{1}{\sqrt{n+1}+\sqrt{n}}$)=2($\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+…+$\sqrt{n+1}$-$\sqrt{n}$)=2($\sqrt{n+1}$-1).
解答 证明:1+$\frac{1}{\sqrt{2}}$+$\frac{1}{\sqrt{3}}$+…+$\frac{1}{\sqrt{n}}$=2($\frac{1}{2}$+$\frac{1}{2\sqrt{2}}$+…+$\frac{1}{2\sqrt{n}}$)>2($\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+…+$\frac{1}{\sqrt{n+1}+\sqrt{n}}$)
=2($\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+…+$\sqrt{n+1}$-$\sqrt{n}$)=2($\sqrt{n+1}$-1).
∴1+$\frac{1}{\sqrt{2}}$+$\frac{1}{\sqrt{3}}$+…+$\frac{1}{\sqrt{n}}$>2($\sqrt{n+1}$-1).
点评 考查放缩法证明不等式的方法,想着用放缩法的原因是:不等式右边是2($\sqrt{n+1}$-1),所以不等式左边提取2,并想法消去中间项,这样便可以想着用放缩法.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案| A. | $\frac{5}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
| A. | 三角形 | B. | 梯形 | C. | 菱形 | D. | 平面四边形 |
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
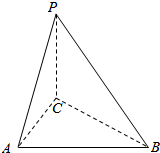 如图所示,三棱锥P-ABC中,平面PAB⊥底面ABC,且PA=PB=PC,则△ABC是直角三角形.
如图所示,三棱锥P-ABC中,平面PAB⊥底面ABC,且PA=PB=PC,则△ABC是直角三角形.