题目内容
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,焦距为2.
,焦距为2.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 的另一个交点为点
的另一个交点为点![]() ,与圆
,与圆![]() 的另一个交点为点
的另一个交点为点![]() ,是否存在直线
,是否存在直线![]() 使得
使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(1)![]() .(2)直线
.(2)直线![]() 不存在.见解析
不存在.见解析
【解析】
(1)据题意有![]() ,
,![]() ,则通过计算可得椭圆
,则通过计算可得椭圆![]() 的标准方程;
的标准方程;
(2)可先假设直线![]() 存在,可设直线
存在,可设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() .根据
.根据![]() 及圆的性质可知
及圆的性质可知![]() 垂直平分
垂直平分![]() .再根据点到直线的距离公式可得
.再根据点到直线的距离公式可得![]() 的关于
的关于![]() 的表达式,再解
的表达式,再解![]() 可得
可得![]() 的关于
的关于![]() 的表达式.然后联立直线与椭圆方程,消去
的表达式.然后联立直线与椭圆方程,消去![]() 整理可得一元二次方程,根据韦达定理有
整理可得一元二次方程,根据韦达定理有![]() ,
,![]() .根据弦长公式可得
.根据弦长公式可得![]() 的关于
的关于![]() 的另一个表达式.根据存在性则两个表达式相等,如果
的另一个表达式.根据存在性则两个表达式相等,如果![]() 值存在则直线存在;如果没有
值存在则直线存在;如果没有![]() 值则直线不存在.
值则直线不存在.
(1)由题意,可知![]() ,
,![]() .则
.则![]() ,
,![]() .
.
![]() 椭圆
椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)由题意,假设存在直线![]() 使得
使得![]() ,可设直线
,可设直线![]() 的斜率为
的斜率为![]() .
.
则直线![]() .
.
![]() ,即点
,即点![]() 为线段
为线段![]() 中点,
中点,
![]() 根据圆的性质,可知
根据圆的性质,可知![]() ,且
,且![]() 平分
平分![]() .
.
根据题意画图如下:
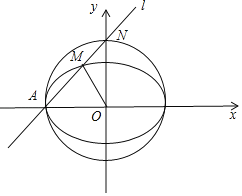
则![]() .
.
在![]() 中,
中,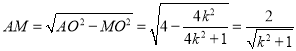 .
.
联立直线![]() 与椭圆
与椭圆![]() 方程,可得:
方程,可得:
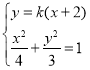 ,
,
消去![]() ,整理得
,整理得![]() .
.
则△![]() .
.
![]() ,
,![]() .
.
![]()
![]()
![]() .
.
![]()
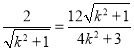 ,整理,得
,整理,得![]() .很明显矛盾,
.很明显矛盾,
故直线![]() 不存在.
不存在.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
【题目】某学校需要从甲、乙两名学生中选一人参加数学竞赛,抽取了近期两人![]() 次数学考试的成绩,统计结果如下表:
次数学考试的成绩,统计结果如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
甲的成绩(分) |
|
|
|
|
|
乙的成绩(分) |
|
|
|
|
|
(1)若从甲、乙两人中选出一人参加数学竞赛,你认为选谁合适?请说明理由.
(2)若数学竞赛分初赛和复赛,在初赛中有两种答题方案:
方案一:每人从![]() 道备选题中任意抽出
道备选题中任意抽出![]() 道,若答对,则可参加复赛,否则被淘汰.
道,若答对,则可参加复赛,否则被淘汰.
方案二:每人从![]() 道备选题中任意抽出
道备选题中任意抽出![]() 道,若至少答对其中
道,若至少答对其中![]() 道,则可参加复赛,否则被润汰.
道,则可参加复赛,否则被润汰.
已知学生甲、乙都只会![]() 道备选题中的
道备选题中的![]() 道,那么你推荐的选手选择哪种答题方条进人复赛的可能性更大?并说明理由.
道,那么你推荐的选手选择哪种答题方条进人复赛的可能性更大?并说明理由.

