题目内容
设函数f(x)=
•
,其中向量
=(-
cosx,cosx+sinx),
=(sinx,
),x∈R.
(1)求函数f(x)的最小正周期与单调递减区间;
(2)求函数f(x)的最小值.
| m |
| n |
| m |
| 3 |
| n |
| cosx-sinx |
| 2 |
(1)求函数f(x)的最小正周期与单调递减区间;
(2)求函数f(x)的最小值.
考点:两角和与差的正弦函数,平面向量数量积的运算,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:利用平面向量的数量积的坐标运算可得f(x)=-
cosxsinx+(cosx+sinx)•
,再利用三角恒等变换,化简可得f(x)=-sin(2x-
),
(1)由正弦函数的周期性与单调性即可求得函数f(x)的最小正周期与单调递减区间;
(2)利用正弦函数的最值的性质,由2x-
=2kπ+
(k∈Z)即可求得f(x)取最小值时相应的x的集合.
| 3 |
| cosx-sinx |
| 2 |
| π |
| 6 |
(1)由正弦函数的周期性与单调性即可求得函数f(x)的最小正周期与单调递减区间;
(2)利用正弦函数的最值的性质,由2x-
| π |
| 6 |
| π |
| 2 |
解答:
(本小题满分12分)
解:由已知得 f(x)=-
sin2x+
(cos2x-sin2x)=-
sin2x+
cos2x=-sin(2x-
)…(4分)
(1)f(x)的最小正周期为T=π…(6分)
当2kπ-
≤2x-
≤2kπ+
即kπ-
≤x≤kπ+
时,f(x)是减函数…(8分)
∴f(x)的减区间为[kπ-
,kπ+
],k∈Z…(9分)
(2)当2x-
=2kπ+
即x=kπ+
时,f(x)取得最小值-1,…(11分)
∴f(x)的最小值为-1,且相应的x的集合为{x|x=kπ+
,k∈Z}…(12分)
解:由已知得 f(x)=-
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
(1)f(x)的最小正周期为T=π…(6分)
当2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
∴f(x)的减区间为[kπ-
| π |
| 6 |
| π |
| 3 |
(2)当2x-
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
∴f(x)的最小值为-1,且相应的x的集合为{x|x=kπ+
| π |
| 3 |
点评:本题考查平面向量数量积的坐标运算,考查三角恒等变换的应用,突出考查正弦函数的周期性、单调性与最值,考查转化思想与运算求解能力.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
函数f(x)=x+
在区间[1,3]上的最小值是( )
| 4 |
| x |
| A、3 | ||
| B、5 | ||
| C、4 | ||
D、
|

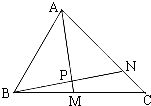 如图所示,在△ABC中,点M是BC的中点,点N在AC上,且AN=2NC,AM与BN交于点P,求AP:PM与BP:PN的值.
如图所示,在△ABC中,点M是BC的中点,点N在AC上,且AN=2NC,AM与BN交于点P,求AP:PM与BP:PN的值.