Question

12、若函数f（x）是定义在R上的偶函数，在（-∞，0]上是减函数，且f（-3）=0，则使得x[f（x）+f（-x）]＜0的x的取值范围是

（-∞，-3）∪（0，3）

．

Answer 1

分析：由f（x）是定义在R上的偶函数，将x[f（x）+f（-x）]＜0转化为xf（x）＜0，再根据在（-∞，0]上是减函数，且f（-3）=0
用特殊图象法来求解．

解答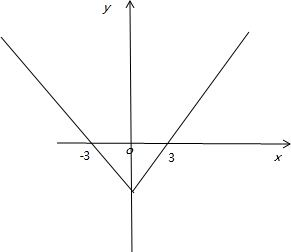：解：∵f（x）是定义在R上的偶函数
∴f（x）+f（-x）=2f（x）
∴x[f（x）+f（-x）]＜0
转化为：xf（x）＜0
又∵在（-∞，0]上是减函数，且f（-3）=0
可作出一个满足函数的图象：
如图所示：x[f（x）+f（-x）]＜0的x的取值范围是：（-∞，-3）∪（0，3）
故答案为：（-∞，-3）∪（0，3）

点评：本题主要考查函数的奇偶性与单调性的综合运用，还考查学生的转化能力，数形结合的能力．