题目内容
定义在R上的函数f(x)满足f(x)=f(x+2),当x∈[1,3]时,f(x)=2-|x-2|,则( )
A、f(sin
| ||||
B、f(sin
| ||||
C、f(cos
| ||||
D、f(tan
|
分析:根据函数的周期性和对称轴,即可得到结论.
解答:解:由f(x)=f(x+2),∴函数f(x)的周期为2.
当x∈[1,3]时,f(x)=2-|x-2|,则函数f(x)关于x=2对称.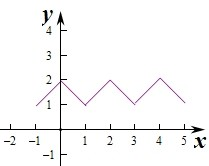
A.f(sin
)=f(
),f(sin
)=f(
),此时.f(sin
)<f(sin
),A错误.
B.f(sin
)=f(
),f(cos
)=f(-
)=f(
),此时f(sin
)<f(cos
),∴B正确.
C.f(cos
)=f(
),f(cos
)=f(
),∴f(cos
)>f(cos
),∴C错误.
D.f(tan
)=f(
),f(tan
)=f(1),∴f(tan
)>f(tan
)∴D错误.
故选:B.
当x∈[1,3]时,f(x)=2-|x-2|,则函数f(x)关于x=2对称.

A.f(sin
| π |
| 3 |
| ||
| 2 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 6 |
B.f(sin
| 2π |
| 3 |
| ||
| 2 |
| 2π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2π |
| 3 |
| 2π |
| 3 |
C.f(cos
| π |
| 3 |
| 1 |
| 2 |
| π |
| 4 |
| ||
| 2 |
| π |
| 3 |
| π |
| 4 |
D.f(tan
| π |
| 6 |
| ||
| 3 |
| π |
| 4 |
| π |
| 6 |
| π |
| 4 |
故选:B.
点评:本题主要考查函数奇偶性和周期性的应用,利用数形结合得到函数的单调性和对称性是解决本题的关键,要求熟练掌握常见三角函数的三角值.

练习册系列答案
相关题目