题目内容
【题目】如图，在四棱柱
中，四边形ABCD是边长等于2的菱形，
，
平面ABCD，O，E分别是
，AB的中点，AC交DE于点H，点F为HC的中点
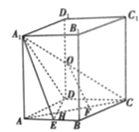
（1）求证：
平面
；
（2）若OF与平面ABCD所成的角为60°，求三棱锥
的表面积.
【答案】（1）证明见解析；（2）
.
【解析】
(1) 连接
，由三角形的中位线可知
，由线面平行的判定定理即可证明
平面
.
(2) 连接BD，通过线面角可求出
，
；由线面垂直的性质可知
，从而分别求出各个面的面积，即可求三棱锥的表面积.
（1）连接，因为点F为HC的中点，O是
的中点，所以，
因为
平面，
平面，所以平面.
（2）连接BD，因为四边形ABCD是边长等于2的菱形，
，
所以是
等边三角形，所以
，
且
.
因为OF与平面ABCD所成的角为60°，且，
平面ABCD，
所以
，所以，，
因为平面ABCD，
平面ABCD，所以
，
又，
，
，
平面
，
所以
平面，又
平面，所以.
故三棱锥
的表面积
.
【题目】已知鲜切花
的质量等级按照花枝长度
进行划分，划分标准如下表所示.
花枝长度 |
|
|
|
鲜花等级 | 三级 | 二级 | 一级 |
某鲜切花加工企业分别从甲乙两个种植基地购进鲜切花，现从两个种植基地购进的鲜切花中分别随机抽取30个样品，测量花枝长度并进行等级评定，所抽取样品数据如图所示.
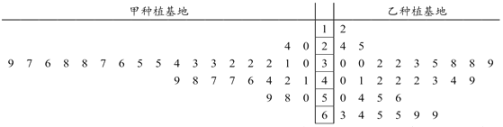
（1）根据茎叶图比较两个种植基地鲜切花的花枝长度的平均值及分散程度(不要求计算具体值，给出结论即可)；
（2）若从等级为三级的样品中随机选取2个进行新产品试加工，求选取的2个全部来自乙种植基地的概率；
（3）根据该加工企业的加工和销售记录，了解到来自乙种植基地的鲜切花的加工产品的单件利润为4元；来自乙种植基地的鲜切花的加工产品的单件成本为10元，销售率(某等级产品的销量与产量的比值)及单价如下表所示.
三级花加工产品 | 二级花加工产品 | 一级花加工产品 | |
销售率 |
|
|
|
单价/(元/件) | 12 | 16 | 20 |
由于鲜切花加工产品的保鲜特点，未售出的产品均可按原售价的50%处理完毕.用样本估计总体，如果仅从单件产品的利润的角度考虑，该鲜切花加工企业应该从哪个种植基地购进鲜切花？