题目内容
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,过
,过![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 的周长为8.
的周长为8.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)问:![]() 的内切圆面积是否有最大值?若有,试求出最大值;若没有,说明理由.
的内切圆面积是否有最大值?若有,试求出最大值;若没有,说明理由.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由离心率得![]() ,再利用
,再利用![]() 的周长为8得
的周长为8得![]() ,从而得到
,从而得到![]() 的值,进而得到椭圆的方程;
的值,进而得到椭圆的方程;
(2)将![]() 的内切圆面积的最大值转化为求
的内切圆面积的最大值转化为求![]() 的值最大,设
的值最大,设![]() ,
,![]() ,直线
,直线![]() ,从而将面积表示成关于
,从而将面积表示成关于![]() 的函数,再利用换元法研究函数的最值.
的函数,再利用换元法研究函数的最值.
(1)![]() 离心率为
离心率为![]() ,
,![]()
![]() ,
,
![]()
![]() 的周长为8,
的周长为8,![]()
![]() ,得
,得![]() ,
,
![]()
![]() ,
,![]() ,
,
因此,椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)设![]() 的内切圆半径为
的内切圆半径为![]() ,
,![]()
![]() ,
,
又![]()
![]() ,
,![]()
![]() ,
,
要使![]() 的内切圆面积最大,只需
的内切圆面积最大,只需![]() 的值最大.
的值最大.
设![]() ,
,![]() ,直线
,直线![]() ,
,
联立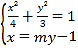 消去
消去![]() 得:
得:![]() ,
,
易得![]() ,且
,且![]() ,
,![]() ,
,
所以![]()
![]() ,
,
设![]() ,则
,则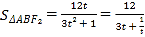 ,
,
设![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
所以当![]() ,即
,即![]() 时,
时,![]() 的最大值为3,
的最大值为3,
此时![]() ,所以
,所以![]() 的内切圆面积最大为
的内切圆面积最大为![]() .
.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯,由此催生了一批外卖点餐平台.已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取100名点外卖的用户进行统计,按送餐距离分类统计结果如表:
送餐距离(千米) | (0,1] | (1,2] | (2,3] | (3,4] | (4,5] |
频数 | 15 | 25 | 25 | 20 | 15 |
以这100名用户送餐距离位于各区间的频率代替送餐距离位于该区间的概率.
(1)若某送餐员一天送餐的总距离为100千米,试估计该送餐员一天的送餐份数;(四舍五入精确到整数,且同一组中的数据用该组区间的中点值为代表).
(2)若该外卖平台给送餐员的送餐费用与送餐距离有关,规定2千米内为短距离,每份3元,2千米到4千米为中距离,每份7元,超过4千米为远距离,每份12元.记X为送餐员送一份外卖的收入(单位:元),求X的分布列和数学期望.
【题目】某城市对一项惠民市政工程满意程度(分值:![]() 分)进行网上调查,有2000位市民参加了投票,经统计,得到如下频率分布直方图(部分图):
分)进行网上调查,有2000位市民参加了投票,经统计,得到如下频率分布直方图(部分图):

现用分层抽样的方法从所有参与网上投票的市民中随机抽取![]() 位市民召开座谈会,其中满意程度在
位市民召开座谈会,其中满意程度在![]() 的有5人.
的有5人.
(1)求![]() 的值,并填写下表(2000位参与投票分数和人数分布统计);
的值,并填写下表(2000位参与投票分数和人数分布统计);
满意程度(分数) |
|
|
|
|
|
人数 |
(2)求市民投票满意程度的平均分(各分数段取中点值);
(3)若满意程度在![]() 的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求男性甲或女性乙被选中的概率.
的5人中恰有2位为女性,座谈会将从这5位市民中任选两位发言,求男性甲或女性乙被选中的概率.
【题目】2020年4月8日零时正式解除离汉通道管控,这标志着封城76天的武汉打开城门了.在疫情防控常态下,武汉市有序复工复产复市,但是仍然不能麻痹大意,仍然要保持警惕,严密防范、慎终如始.为科学合理地做好小区管理工作,结合复工复产复市的实际需要,某小区物业提供了![]() ,
,![]() 两种小区管理方案,为了了解哪一种方案最为合理有效,物业随机调查了50名男业主和50名女业主,每位业主对
两种小区管理方案,为了了解哪一种方案最为合理有效,物业随机调查了50名男业主和50名女业主,每位业主对![]() ,
,![]() 两种小区管理方案进行了投票(只能投给一种方案),得到下面的列联表:
两种小区管理方案进行了投票(只能投给一种方案),得到下面的列联表:
|
| |
男业主 | 35 | 15 |
女业主 | 25 | 25 |
(1)分别估计![]() ,
,![]() 方案获得业主投票的概率;
方案获得业主投票的概率;
(2)判断能否有95%的把握认为投票选取管理方案与性别有关.
附: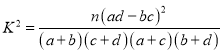 .
.
|
|
|
|
|
|
|
|