题目内容
【题目】如图,某市有相交于点O的一条东西走向的公路l,与南北走向的公路m,这两条公路都与一块半径为1(单位:千米)的圆形商城A相切.根据市民建议,欲再新建一条公路PQ,点P、Q分别在公路l、m上,且要求PQ与圆形商城A也相切.
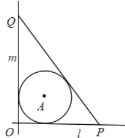
(1)当P距O处4千米时,求OQ的长;
(2)当公路PQ长最短时,求OQ的长.
【答案】(1) 3千米.(2) ![]() 千米
千米
【解析】
(1)先建立以O为原点,直线l、m分别为x,y轴建立平面直角坐标系.设直线方程为:![]() ,由直线与圆的位置关系可得
,由直线与圆的位置关系可得![]() ,运算即可得解;
,运算即可得解;
(2)设![]() ,
,![]()
![]() ,由PQ与圆A相切,得
,由PQ与圆A相切,得![]() ,再结合重要不等式即可得解.
,再结合重要不等式即可得解.
解:(1)以O为原点,直线l、m分别为x,y轴建立平面直角坐标系.
设PQ与圆A相切于点B,连结AB,以1千米为单位长度,
则圆A的方程为![]() ,
,
由题意可设直线PQ的方程为![]() ,即
,即![]() ,
,![]() ,
,
∵PQ与圆A相切,∴![]() ,解得
,解得![]() ,
,
故当P距O处4千米时,OQ的长为3千米.
(2)设![]() ,
,![]()
![]() ,
,
则直线PQ方程为![]() ,即
,即![]() .
.
因为PQ与圆A相切,所以![]() ,
,
化简得![]() ,即
,即![]() ;
;
解法一:因此![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() ,于是
,于是![]() .
.
又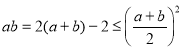 ,解得
,解得![]() ,或
,或![]()
因为![]() ,所以
,所以![]() ,
,
![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
所以PQ最小值为![]() ,此时
,此时![]() .
.
答:当P、Q两点距离两公路的交点O都为![]() (千米)时,新建公路PQ最短.
(千米)时,新建公路PQ最短.
解法二:
化简得![]() ,即
,即![]() .
.
因为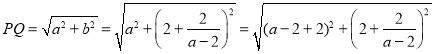
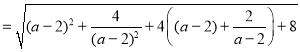
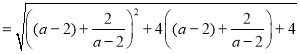
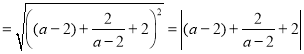
因为![]() ,所以
,所以![]() .
.
当且仅当![]() ,即
,即![]() 时取到等号,
时取到等号,
答:当P、Q两点距离两公路的交点O都为![]() (千米)时,新建公路PQ最短.
(千米)时,新建公路PQ最短.
解法三:设PQ与圆A相切于点B,连结AB、AP、AQ,设![]() ,
,
则![]() ,
,![]() ,且
,且![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() ,
,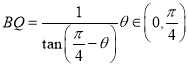
∴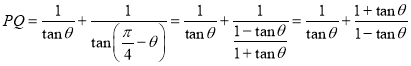
![]()
![]()
(当且仅当![]() 取等号)
取等号)
答:当P、Q两点距离两公路的交点O都为![]() (千米)时,新建公路PQ最短.
(千米)时,新建公路PQ最短.
解法四:设PQ与![]() 相切于点B,设
相切于点B,设![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
在![]() 中,由
中,由![]() 得:
得:![]() ,
,
化简得:![]() ,∴
,∴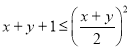 ,
,
解得:![]() 或
或![]() (舍)
(舍)
(当且仅当![]() 时等号成立)
时等号成立)
∴当![]() 时,PQ有最小值;
时,PQ有最小值;
答:当P、Q两点距离公路交点O都为![]() (千米)时,新建公路PQ最短.
(千米)时,新建公路PQ最短.