题目内容
【题目】设A，B，C，D为平面内的四点，且A（1，3），B（2，﹣2），C（4，1）．
（1）若 
= 
，求D点的坐标；
（2）设向量 
= ， 
= 
，若k ﹣ 与 +3 平行，求实数k的值．
【答案】
（1）解：设D（x，y）．∵ 
，
∴（2，﹣2）﹣（1，3）=（x，y）﹣（4，1），
化为（1，﹣5）=（x﹣4，y﹣1），
∴ 
，解得 
，
∴D（5，﹣4）．
（2）解：∵ 
=（1，﹣5）， 
= 
=（4，1）﹣（2，﹣2）=（2，3）．
∴ 
=k（1，﹣5）﹣（2，3）=（k﹣2，﹣5k﹣3）， 
=（1，﹣5）+3（2，3）=（7，4）．
∵k 
﹣ 与 +3 平行，
∴7（﹣5k﹣3）﹣4（k﹣2）=0，解得k= 
．
∴ 
【解析】（1）利用向量相等即可得出；（2）利用向量共线定理即可得出．
【题目】某种产品的广告费支出x与销售额y（单位：百万元）之间有如下对应数据：
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 50 | 60 | 70 |
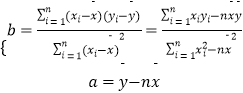
（1）画出散点图；
（2）求线性回归方程；
（3）预测当广告费支出为7百万元时的销售额．参考公式：．
【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系，对该校200名高三学生的课外体育锻炼平均每天运动的时间进行调查，如表：（平均每天锻炼的时间单位：分钟）
平均每天锻炼 | [0，10） | [10，20） | [20，30） | [30，40） | [40，50） | [50，60） |
总人数 | 20 | 36 | 44 | 50 | 40 | 10 |
将学生日均课外课外体育运动时间在[40，60）上的学生评价为“课外体育达标”．
（1）请根据上述表格中的统计数据填写下面2×2列联表，并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关？
课外体育不达标 | 课外体育达标 | 合计 | |
男 | |||
女 | 20 | 110 | |
合计 |
（2）将上述调查所得到的频率视为概率．现在从该校高三学生中，抽取3名学生，记被抽取的3名学生中的“课外体育达标”学生人数为X，若每次抽取的结果是相互独立的，求X的数学期望和方差．
参考公式： 
，其中n=a+b+c+d．
参考数据：
P（K2≥k0） | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
