题目内容
20.已知在平面直角坐标系中,点P是直线l:l=-$\frac{1}{2}$上一动点,定点F($\frac{1}{2}$,0),点Q为PF的中点,动点M满足$\overrightarrow{MQ}$•$\overrightarrow{PF}$=0,$\overrightarrow{MP}$=λ$\overrightarrow{OF}$(λ∈R).过点M作圆(x-3)2+y2=2的切线,切点分别为S,T,则$\overrightarrow{MS}$•$\overrightarrow{MT}$的最小值是( )| A. | $\frac{3}{5}$ | B. | $\frac{35}{9}$ | C. | $\frac{10}{3}$ | D. | -$\frac{1}{3}$ |
分析 由题意结合平面向量的数量积运算求得M在抛物线y2=2x上,则问题转化为过抛物线上一点,作圆(x-3)2+y2=2的切线,切点分别为S,T,求$\overrightarrow{MS}$•$\overrightarrow{MT}$的最小值,然后求出满足条件的点M,代入平面向量数量积求解.
解答 解:如图,设P($-\frac{1}{2}$,m),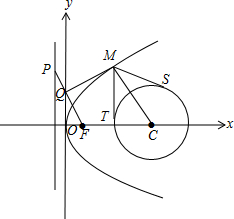 ∵F($\frac{1}{2}$,0),点Q为PF的中点,∴Q(0,$\frac{m}{2}$),
∵F($\frac{1}{2}$,0),点Q为PF的中点,∴Q(0,$\frac{m}{2}$),
再设M(x0,y0),
∴$\overrightarrow{MP}=(-\frac{1}{2}-{x}_{0},m-{y}_{0})$,$\overrightarrow{OF}=(\frac{1}{2},0)$,
由$\overrightarrow{MP}$=λ$\overrightarrow{OF}$,得$(-\frac{1}{2}-{x}_{0},m-{y}_{0})=(\frac{1}{2}λ,0)$,即$\left\{\begin{array}{l}{-\frac{1}{2}-{x}_{0}=\frac{1}{2}λ}\\{m-{y}_{0}=0}\end{array}\right.$,
∴M($-\frac{1}{2}-\frac{1}{2}λ,m$),
则$\overrightarrow{MQ}=(\frac{1}{2}+\frac{1}{2}λ,-\frac{m}{2})$,$\overrightarrow{PF}=(1,-m)$.
再由$\overrightarrow{MQ}$•$\overrightarrow{PF}$=0,得$\frac{1}{2}+\frac{1}{2}λ+\frac{{m}^{2}}{2}=0$,即$-\frac{1}{2}-\frac{1}{2}λ=\frac{{m}^{2}}{2}$,
∴M($\frac{{m}^{2}}{2},m$),则M在抛物线y2=2x上,
设以(3,0)为圆心,以r为半径的圆为(x-3)2+y2=r2,
联立$\left\{\begin{array}{l}{{y}^{2}=2x}\\{(x-3)^{2}+{y}^{2}={r}^{2}}\end{array}\right.$,得x2-4x+9-r2=0.
由△=(-4)2-4(9-r2)=0,解得r2=5.
∴r=$\sqrt{5}$.
则抛物线y2=2x上的点M到圆心距离的最小值为$\sqrt{5}$,切线长的最小值为$\sqrt{3}$,
且sin$∠SMC=\sqrt{\frac{2}{5}}$,cos∠SMT=1-2sin2∠SMC=1-$\frac{4}{5}=\frac{1}{5}$.
∴$\overrightarrow{MS}$•$\overrightarrow{MT}$的最小值为$|\overrightarrow{MS}|•|\overrightarrow{MT}|•cos∠SMT$=$\sqrt{3}×\sqrt{3}×\frac{1}{5}=\frac{3}{5}$.
故选:A.
点评 本题考查了圆的切线方程,考查了平面向量的数量积运算,考查了数学转化思想方法,综合性较强,是难题.


| A. | $\frac{3}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{5}{6}$ | D. | 5 |
| A. | 2 | B. | 3 | C. | 4 | D. | 3+2$\sqrt{2}$ |

| A. | $\frac{2011}{2012}$ | B. | $\frac{1}{2012}$ | C. | $\frac{2012}{2013}$ | D. | $\frac{1}{2013}$ |
| A. | $\frac{\sqrt{3}-1}{2}$ | B. | $\frac{1+\sqrt{3}}{2}$ | C. | $\frac{2+\sqrt{6}}{2}$ | D. | $\frac{\sqrt{6}-2}{2}$ |