题目内容
20.若二次函数f(x)=x2+mx-(m-1)的图象与x轴有两个交点,则实数m的取值范围是m>-2+2$\sqrt{2}$或m<-2-2$\sqrt{2}$.分析 二次函数f(x)=x2+mx-(m-1)的图象与x轴有两个交点,相当于方程x2+mx-(m-1)=0有两不同实数根,
可得∴△=m2+4(m-1)>0,根据求根公式可得m的范围.
解答 解:二次函数f(x)=x2+mx-(m-1)的图象与x轴有两个交点,
∴方程x2+mx-(m-1)=0有两不同实数根,
∴△=m2+4(m-1)>0,
∴m>-2+2$\sqrt{2}$或m<-2-2$\sqrt{2}$,
故答案为m>-2+2$\sqrt{2}$或m<-2-2$\sqrt{2}$.
点评 考查了二次函数的图象和函数与方程的关系,利用求根公式解二次不等式问题.属于基础题型,应熟练掌握.

练习册系列答案
相关题目
11.设函数y=lnx与y=ax2-a的图象有公共点.且在公共点处有共同的切线.则a的值为( )
| A. | $\frac{e}{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | 1或$\frac{1}{2}$ |
8.已知θ∈R,向量$\overrightarrow{a}$=(sinθ,cosθ),$\overrightarrow{b}$=(2,1),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则sin2θ( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{2}{5}$ | D. | -$\frac{2}{5}$ |
12.若sinα+cosα=$\frac{\sqrt{5}}{5}$(α是第二象限角),则tanα的值是( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{2}{5}$ |
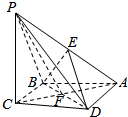 已知四棱锥P-ABCD中,四边形ABCD是边长为2的菱形,AC交BD于F,E为PA的中点,PC=3,且PC⊥平面ABCD.
已知四棱锥P-ABCD中,四边形ABCD是边长为2的菱形,AC交BD于F,E为PA的中点,PC=3,且PC⊥平面ABCD.