题目内容
11.设函数y=lnx与y=ax2-a的图象有公共点.且在公共点处有共同的切线.则a的值为( )| A. | $\frac{e}{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | 1或$\frac{1}{2}$ |
分析 设公共点P(x0,y0),则lnx0=ax02-a①,f′(x0)=g′(x0),联立消掉a可得关于x0的方程,构造函数,根据函数单调性可求得唯一x0值,进而可求a的值.
解答 解:设公共点P(x0,y0),则lnx0=ax02-a①,
f′(x0)=g′(x0),即$\frac{1}{{x}_{0}}$=2ax0,化简得1=2ax02②,
联立①②消a得,lnx0=$\frac{1}{2}$-$\frac{1}{2{{x}_{0}}^{2}}$,
令φ(x)=lnx-$\frac{1}{2}$+$\frac{1}{2{x}^{2}}$,φ′(x)=$\frac{1}{x}$-$\frac{1}{{x}^{3}}$=$\frac{(x-1)(x+1)}{{x}^{3}}$,
由②可得a>0,
易知φ(x)在(0,1]递减,[1,+∞)上单调递增,又φ(1)=0,
所以φ(x)=lnx-$\frac{1}{2}$+$\frac{1}{2{x}^{2}}$=0有唯一解1,即x0=1,
则y0=ln1=0,a=$\frac{1}{2}$.
故选:C.
点评 本题考查利用导数研究函数的单调性及导数的几何意义,考查学生灵活运用所学知识分析问题解决问题的能力,属于中档题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
2.设0≤x≤2π,则函数f(x)=cos2x+4sinx-1的最大值为( )
| A. | 5 | B. | 3 | C. | -5 | D. | 4 |
6.把一颗骰子投掷两次,观察出现的点数,并记第一次出现的点数为a,第二次出现的点数为b,向量$\overrightarrow{m}$=(a,b),$\overrightarrow{n}$=(1,2),则向量$\overrightarrow{m}$与向量$\overrightarrow{n}$不共线的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{12}$ | C. | $\frac{11}{12}$ | D. | $\frac{1}{18}$ |
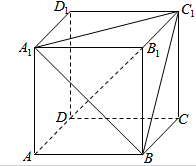 求证:正方体ABCD-A1B1C1D1中,对角线B1D与平面A1BC1互相垂直.
求证:正方体ABCD-A1B1C1D1中,对角线B1D与平面A1BC1互相垂直.