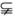Question

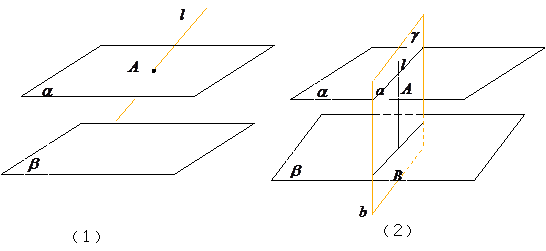
求证:如果一条直线与两个相交的平面都平行,那么这条直线与这两个平面的交线平行.

已知:a∥α,a∥β,α∩β=b.

求证:a∥b.

Answer 1

思路点拨：已知线面平行,容易想到利用线面平行的性质,从而得到线线平行,而要利用线面平行的性质就要考虑添加辅助面.

证明：在平面α内任取一点P(Pb)，平面β内取一点Q(Qb).设过点P和直线a的平面为α₁,α₁∩α=c.过点Q和直线b的平面为β₁,β₁∩β=d.

因为a∥α,所以a∥c.

又因为a∥β,所以a∥d.故c∥d.

又dβ，所以c∥β.

因为α∩β=b，所以c∥b.

又a∥c（已证）,故a∥b.

［一通百通］ 有关证明线线平行的问题，通常可以考虑先通过证明相关的线面平行,从而利用线面平行的性质定理而得到线线平行.