题目内容
椭圆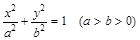 的离心率是
的离心率是 ,它被直线
,它被直线 截得的弦长是
截得的弦长是 ,求椭圆的方程.
,求椭圆的方程.
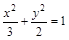
解析试题分析:求椭圆方程基本方法为待定系数法,两个未知数只需列出两个独立条件.根据离心率是 ,得到
,得到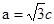 .根据椭圆被直线截得的弦长,可列出第二个等式.由直线方程与椭圆方程联立方程组消去y得
.根据椭圆被直线截得的弦长,可列出第二个等式.由直线方程与椭圆方程联立方程组消去y得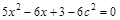 ,结合韦达定理及弦长公式可得c=1.
,结合韦达定理及弦长公式可得c=1.
试题解析:解: ∵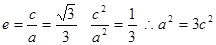
∴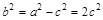 ∴椭圆方程可写为
∴椭圆方程可写为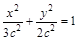 2分
2分
将直线方程 代入椭圆方程,消去y,整理得
代入椭圆方程,消去y,整理得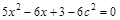 依韦达定理得
依韦达定理得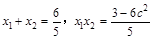 6分
6分
∴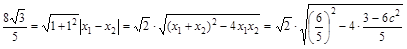
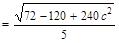 解得c=1 ∴a2=3,b2=2. ∴椭圆方程为
解得c=1 ∴a2=3,b2=2. ∴椭圆方程为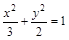 12分
12分
考点:直线与椭圆位置关系

练习册系列答案
相关题目
 经过点
经过点 ,且两焦点与短轴的两个端点的连线构成一正方形.
,且两焦点与短轴的两个端点的连线构成一正方形. 的方程;
的方程; 与椭圆
与椭圆 交于
交于 ,
, 两点,若线段
两点,若线段 的垂直平分线经过点
的垂直平分线经过点 ,求
,求
 为原点)面积的最大值.
为原点)面积的最大值. 的一个顶点为B(0,4),离心率
的一个顶点为B(0,4),离心率 ,直线
,直线 交椭圆于M,N两点。
交椭圆于M,N两点。 ,求弦MN的长;
,求弦MN的长;
 的最大值
的最大值 :
: 的切线l,切点A在第二象限。
的切线l,切点A在第二象限。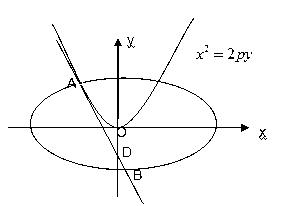
 的椭圆
的椭圆 恰好经过A点,设切线l交椭圆的另一点为B,若设切线l,直线OA,OB的斜率为k,
恰好经过A点,设切线l交椭圆的另一点为B,若设切线l,直线OA,OB的斜率为k, ,①试用斜率k表示
,①试用斜率k表示 ②当
②当 ,在y轴上截得线段长为2
,在y轴上截得线段长为2 .
. ,求圆P的方程.
,求圆P的方程. 的焦点为
的焦点为 ,点
,点 ,线段
,线段 的中点在抛物线上. 设动直线
的中点在抛物线上. 设动直线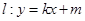 与抛物线相切于点
与抛物线相切于点 ,且与抛物线的准线相交于点
,且与抛物线的准线相交于点 ,以
,以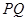 为直径的圆记为圆
为直径的圆记为圆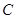 .
. 的值;
的值; 轴必有公共点;
轴必有公共点; ,使得圆
,使得圆 +
+ =1(a>b>0),称圆心在原点O,半径为
=1(a>b>0),称圆心在原点O,半径为 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F(
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为F( ,0),其短轴上的一个端点到F的距离为
,0),其短轴上的一个端点到F的距离为 .
. =1的焦距为2,求椭圆上的一点到两个焦点的距离之和.
=1的焦距为2,求椭圆上的一点到两个焦点的距离之和.