题目内容
【题目】设函数![]() ,已知
,已知![]() 在
在![]() 有且仅有3个零点,下列结论正确的是( )
有且仅有3个零点,下列结论正确的是( )
A.在![]() 上存在
上存在![]() ,
,![]() ,满足
,满足![]()
B.![]() 在
在![]() 有且仅有1个最小值点
有且仅有1个最小值点
C.![]() 在
在![]() 单调递增
单调递增
D.![]() 的取值范围是
的取值范围是![]()
【答案】AD
【解析】
对A选项,易知最小正周期![]() ;对D,结合伸缩变换先求
;对D,结合伸缩变换先求![]() 在
在![]() 轴右侧的前4个零点,进而得到
轴右侧的前4个零点,进而得到![]() 在
在![]() 轴右侧的前4个零点,再列出不等式组,即可得
轴右侧的前4个零点,再列出不等式组,即可得![]() 的范围;对B,可以把第三个零点与第四个零点的中点坐标求出来,利用选项D中
的范围;对B,可以把第三个零点与第四个零点的中点坐标求出来,利用选项D中![]() 的范围,可得该中点坐标可能在
的范围,可得该中点坐标可能在![]() 内;对C,根据选项D中
内;对C,根据选项D中![]() 的范围,可得
的范围,可得![]() 的范围不在区间
的范围不在区间![]() 内.
内.
解: 对A,![]() 在
在![]() 有且仅有3个零点,则函数的最小正周期
有且仅有3个零点,则函数的最小正周期![]() ,
,
在![]() 上存在
上存在![]() ,
,![]() ,满足
,满足![]() ,
,
所以![]() 可以成立,故A正确;
可以成立,故A正确;
对D,函数![]() 在
在![]() 轴右侧的前4个零点分别是:
轴右侧的前4个零点分别是:![]() ,
,
则函数![]() 在
在![]() 轴右侧的前4个零点分别是:
轴右侧的前4个零点分别是:![]() ,
,
因为函数![]() 在
在![]() 有且仅有3个零点,
有且仅有3个零点,
所以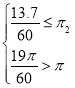
![]() ,故D正确.
,故D正确.
对B,由D选项中前4个零点分别是:![]() ,
,
得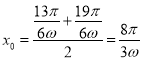 ,
,
此时![]() 可使函数
可使函数![]() 取得最大值,
取得最大值,
因为![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 可能存在2个最小值点,故B错误;
可能存在2个最小值点,故B错误;
对C,由D选项中![]() ,所以
,所以![]() ,
,
区间![]() 不是
不是![]() 的子区间,故C错误.
的子区间,故C错误.
故选: AD

练习册系列答案
相关题目