题目内容
4.设已知T时矩阵$[\begin{array}{l}{a}&{c}\\{b}&{0}\end{array}]$所对应的变换(其中b>0),A(1,0),且T(A)=P,若△POA的面积为$\sqrt{3}$,∠POA=$\frac{π}{3}$,则a+b=2+2$\sqrt{3}$.分析 由$[\begin{array}{l}{a}&{c}\\{b}&{0}\end{array}]$$[\begin{array}{l}{1}\\{0}\end{array}]$=$[\begin{array}{l}{a}\\{b}\end{array}]$,知P(a,b).由b>0,S△POA=$\sqrt{3}$,∠POA=$\frac{π}{3}$,能求出a,b的值.
解答 解:∵$[\begin{array}{l}{a}&{c}\\{b}&{0}\end{array}]$$[\begin{array}{l}{1}\\{0}\end{array}]$=$[\begin{array}{l}{a}\\{b}\end{array}]$,
∴P(a,b). …(5分)
∵b>0,S△POA=$\sqrt{3}$,∠POA=$\frac{π}{3}$,
P(a,b),A(1,0),
∴a=2,b=2$\sqrt{3}$.可得:a+b=2+2$\sqrt{3}$.…(10分)
故答案为:2+2$\sqrt{3}$.
点评 本题考查矩阵变换的性质和应用,解题时要认真审题,仔细解答,属于中档题.

练习册系列答案
相关题目
19.已知集合A={x|x2-2x≤0},B={x|x<m},若A⊆B,则实数m的取值范围是( )
| A. | [2,+∞) | B. | (2,+∞) | C. | (-∞,0) | D. | (-∞,0] |
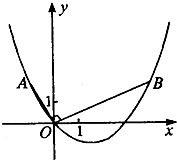 如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标 是(-1,2)
如图,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标 是(-1,2)