题目内容
11.已知某几何体的三视图如图所示,则它的外接球的表面积为5π.
分析 根据三视图判断几何体的形状,根据它的几何性质得出AD⊥面BDC,DC=1,AD=1,BE⊥CD与E,DE=$\frac{1}{2}$,BE=$\frac{\sqrt{3}}{2}$,
利用三角形判断得出三角形BDC外接圆的半径r=1,构造长方体利用外接球的几何性质求解R即得出面积.
解答 解:根据三视图得出几何体为三棱锥,
AD⊥面BDC,DC=1,AD=1,BE⊥CD与E,DE=$\frac{1}{2}$,BE=$\frac{\sqrt{3}}{2}$,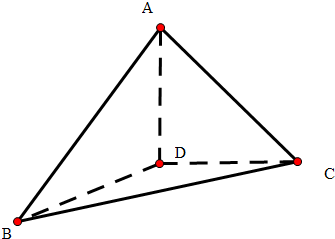
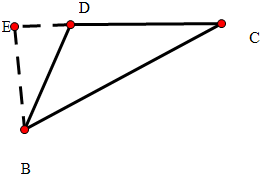
∴∠BDE=60°,BD=1,
∵在三角形BDC中,BD=DC=1,∠BDC=120°,
∴根据余弦定理得出:BC=$\sqrt{3}$,
∵利用正弦定理得出:$\frac{BC}{sin120°}$=2r
∴三角形BDC外接圆的半径r=1,直径为2,
∵三棱锥的外接球的半径R,d=AD=1,
利用球的几何性质得出:△BCD的外接圆的以DC为一边的内接矩形的边长$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
构造长方体棱长为:1,1,$\sqrt{3}$,可知长方体的外接球的直径2R=$\sqrt{{1}^{2}+{1}^{2}+3}$,
即R=$\frac{\sqrt{5}}{2}$,
∴它的外接球的表面积为4×π×( $\frac{\sqrt{5}}{2}$ )2=5π
故答案为:5π.
点评 本题考查了空间几何体的外接球的问题,充分利用几何性质,把立体问题转化为平面问题求解,考查了三角的定理的运用综合性较强,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
19.O为△ABC内一点,$\overrightarrow{AO}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+2μ-1的取值范围为( )
| A. | (-1,1) | B. | (-1,] | C. | [-1,1) | D. | [-1,1] |
6.已知等比数列{an}的各项都是正数,且3a1,$\frac{1}{2}$a3,2a2成等差数列,则$\frac{{a}_{20}+{a}_{19}}{{a}_{18}+{a}_{17}}$=( )
| A. | 1 | B. | 3 | C. | 6 | D. | 9 |
16.已知平面α,β,γ,直线a,b,c,则下列命题正确的是( )
| A. | 若α⊥γ,β⊥γ,则α∥β | B. | 若a⊥c,b⊥c,则a∥b | C. | 若a⊥α,b⊥α,则a∥b | D. | 若a∥α,b∥α,则a∥b |
 如图,某商业中心O有通往正东方向和北偏东30°方向的两条街道,某公园P位于商业中心北偏东θ角(0<θ<$\frac{π}{2}$,tanθ=3$\sqrt{3}$),且与商业中心O的距离为$\sqrt{21}$公里处,现要经过公园P修一条直路分别与两条街道交汇于A,B两处,当商业中心O到A,B两处的距离之和最小时,A,B的距离为3$\sqrt{3}$公里.
如图,某商业中心O有通往正东方向和北偏东30°方向的两条街道,某公园P位于商业中心北偏东θ角(0<θ<$\frac{π}{2}$,tanθ=3$\sqrt{3}$),且与商业中心O的距离为$\sqrt{21}$公里处,现要经过公园P修一条直路分别与两条街道交汇于A,B两处,当商业中心O到A,B两处的距离之和最小时,A,B的距离为3$\sqrt{3}$公里. 如图,四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是梯形,AB∥DC,∠BAD=90°,AB=AD=$\frac{1}{2}$CD=1
如图,四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是梯形,AB∥DC,∠BAD=90°,AB=AD=$\frac{1}{2}$CD=1