题目内容
20. 如图,四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是梯形,AB∥DC,∠BAD=90°,AB=AD=$\frac{1}{2}$CD=1
如图,四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是梯形,AB∥DC,∠BAD=90°,AB=AD=$\frac{1}{2}$CD=1(Ⅰ)求证:平面BCC1⊥平面BDC1;
(Ⅱ)在线段C1D1上是否存在一点P,使AP∥平面BDC1.若存在,请确定点P的位置;若不存在,请说明理由.
分析 (Ⅰ)根据面面垂直的判定定理即可证明平面BCC1⊥平面BDC1;
(Ⅱ)根据线面平行的判定定理进行证明即可得到结论.
解答 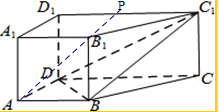 证明:(Ⅰ)因为AA1⊥底面ABCD,所以CC1⊥底面ABCD,
证明:(Ⅰ)因为AA1⊥底面ABCD,所以CC1⊥底面ABCD,
因为BD?底面ABCD,
所以CC1⊥BD,…(2分)
因为底面ABCD是梯形,AB∥DC,∠BAD=90°,
AB=AD=$\frac{1}{2}$CD,
因为AB=1,所以AD=1,CD=2
所以BD=$\sqrt{2}$,BC=$\sqrt{2}$,
所以在△BCD中,BD2+BC2=CD2,
所以∠CBD=90°,
所以BD⊥BC,…(4分)
又因为CC1⊥BD,
所以BD⊥平面BCC1,
因为BD?平面BDC1,
所以平面BCC1⊥平面BDC1,…(6分)
(Ⅱ)存在点P是C1D1的中点,使AP∥平面BDC1 …(8分)
证明如下:取线段C1D1的中点为点P,连结AP,
所以C1D1∥CD,且C1P=$\frac{1}{2}CD$
因为AB∥CD,AB=$\frac{1}{2}$CD,
所以C1P∥AB,且C1P=AB
所以四边形ABC1P是平行四边形.…(10分)
所以AP∥CB1.
又因为BC1?平面BDC1,AP?平面BDC1,
所以AP∥平面BDC1.…(12分)
点评 本题主要考查面面垂直和线面平行的判定,要求熟练掌握相应的判定定理,考查学生的推理能力.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
15.函数f(x)=sin(2ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期为π,且其图象向左平移$\frac{π}{12}$个单位得到的函数图象关于直线x=$\frac{π}{2}$对称,则f($\frac{π}{2}$)=( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
9.某工厂生产某种零件,每日生产成本为1000元,此零件每天的批发价和产量均具有随机性,且互不影响.其具体情况如下表:
(1)设随机变量X表示生产这种零件的日利润,求X的分布列及期望;
(2)若该厂连续3天按此情况生产和销售,设随机变量Y表示这3天中利润不少于3000的天数,求Y的数学期望和方差,并求至少有2天利润不少于3000的概率.(注:以上计算所得概率值用小数表示)
| 日产量 | 400 | 500 | 批发价 | 8 | 10 | |
| 概 率 | 0.4 | 0.6 | 概 率 | 0.5 | 0.5 |
(2)若该厂连续3天按此情况生产和销售,设随机变量Y表示这3天中利润不少于3000的天数,求Y的数学期望和方差,并求至少有2天利润不少于3000的概率.(注:以上计算所得概率值用小数表示)
17. 如图,在网格状小地图中,一机器人从A(0,0)点出发,每秒向上或向右行走1格到相应顶点,已知向上的概率是$\frac{2}{3}$,向右的概率是$\frac{1}{3}$,问6秒后到达B(4,2)点的概率为( )
如图,在网格状小地图中,一机器人从A(0,0)点出发,每秒向上或向右行走1格到相应顶点,已知向上的概率是$\frac{2}{3}$,向右的概率是$\frac{1}{3}$,问6秒后到达B(4,2)点的概率为( )
 如图,在网格状小地图中,一机器人从A(0,0)点出发,每秒向上或向右行走1格到相应顶点,已知向上的概率是$\frac{2}{3}$,向右的概率是$\frac{1}{3}$,问6秒后到达B(4,2)点的概率为( )
如图,在网格状小地图中,一机器人从A(0,0)点出发,每秒向上或向右行走1格到相应顶点,已知向上的概率是$\frac{2}{3}$,向右的概率是$\frac{1}{3}$,问6秒后到达B(4,2)点的概率为( )| A. | $\frac{16}{729}$ | B. | $\frac{80}{243}$ | C. | $\frac{4}{729}$ | D. | $\frac{20}{243}$ |
