题目内容
【题目】过抛物线![]() (其中
(其中![]() )的焦点
)的焦点![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,且
两点,且![]() 两点的纵坐标之积为
两点的纵坐标之积为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)对于![]() 轴上给定的点
轴上给定的点![]() (其中
(其中![]() ),若过点
),若过点![]() 和
和![]() 两点的直线交抛物线
两点的直线交抛物线![]() 的准线
的准线![]() 点,求证:直线
点,求证:直线![]() 与
与![]() 轴交于一定点.
轴交于一定点.
【答案】(1)![]() ; (2)1; (3)见解析.
; (2)1; (3)见解析.
【解析】
(1)设直线AB的方程,联立抛物线方程,运用韦达定理,可得p=4,即得抛物线方程;(2)推理证明![]() =
=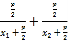 ,整理即可得到所求值;(3)设A(
,整理即可得到所求值;(3)设A(![]() ,y1),B(
,y1),B(![]() ,y2),P(﹣2,s),运用三点共线的条件:斜率相等,可得s,设AP交x轴上的点为(t,0),运用韦达定理,化简整理可得所求定点.
,y2),P(﹣2,s),运用三点共线的条件:斜率相等,可得s,设AP交x轴上的点为(t,0),运用韦达定理,化简整理可得所求定点.
(1)过抛物线![]() (其中
(其中![]() )的焦点
)的焦点![]() 的直线
的直线
为![]() ,代入抛物线方程,可得
,代入抛物线方程,可得![]() ,
,
可设![]() ,
,
即有![]() ,解得
,解得![]() ,
,
可得抛物线的方程为![]() ;
;
(2)由直线![]() 过抛物线的焦点
过抛物线的焦点![]() ,
,
由(1)可得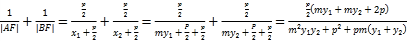 ,将
,将![]() 代入可得
代入可得![]() ;
;
(3)证明:设![]() ,
,![]() ,
,![]() ,
,
由![]() 三点共线可得
三点共线可得
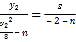 ,可得
,可得![]() ,①
,①
设![]() 交
交![]() 轴上的点为
轴上的点为![]() ,即有
,即有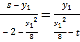 ,
,
代入①,结合![]() ,可得
,可得![]() ,
,
即有![]() ,
,
可得![]() .即有直线
.即有直线![]() 与
与![]() 轴交于一定点
轴交于一定点![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个2×2的列联表;并估计,以运动为主的休闲方式的人的比例;
(2)能否在犯错误的概率不超过0.025的前提下,认为性别与休闲方式有关系?
附表:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2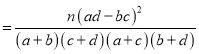 .
.