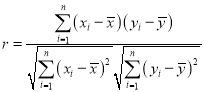题目内容
【题目】已知函数![]()
(1)若![]() ,
,![]() ,若
,若![]() 的单调区间;
的单调区间;
(2)当![]() 时,若
时,若![]() 存在唯一的零点
存在唯一的零点![]() ,且
,且![]() ,其中
,其中![]() ,求
,求![]() .
.
(参考数据:![]() ,
,![]() )
)
【答案】(1)![]() 单调递减区间为
单调递减区间为![]() ,
,![]() 单调递增区间为
单调递增区间为![]() ;(2)
;(2)![]() .
.
【解析】
(1)将![]() ,
,![]() 代入函数
代入函数![]() 解析式,求得
解析式,求得![]() 并令
并令![]() ,即可由导函数的符号判断单调区间.
,即可由导函数的符号判断单调区间.
(2)将![]() 代入函数
代入函数![]() 解析式,求得
解析式,求得![]() .结合定义域及二次函数性质可知
.结合定义域及二次函数性质可知![]() 的单调区间,并根据零点意义代入方程和函数,可得零点的函数表达式.构造函数
的单调区间,并根据零点意义代入方程和函数,可得零点的函数表达式.构造函数![]() ,并求得
,并求得![]() 可证明
可证明![]() 的单调性,结合零点存在定理及所给参考数据,即可求得
的单调性,结合零点存在定理及所给参考数据,即可求得![]() 的值.
的值.
(1)将![]() ,
,![]() 代入函数
代入函数![]() 解析式可得
解析式可得![]() ,定义域为
,定义域为![]() ,
,
则![]()
令![]() ,解得
,解得![]() ,
,![]() (舍),
(舍),
所以当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
故![]() 的单调递减区间为
的单调递减区间为![]() ;
;![]() 的单调递增区间为
的单调递增区间为![]() .
.
(2)将![]() 代入函数
代入函数![]() 解析式可得
解析式可得![]() ,
,
则![]()
因为![]() ,且对于
,且对于![]() 来说,
来说,![]() ,
,
所以![]() 有两个不等式实数根
有两个不等式实数根![]() ,
,
且![]() ,
,
所以两根异号,不妨设![]() 则
则![]() ,
,
则由定义域为![]() 可得
可得![]() 在
在![]() 内递减,在
内递减,在![]() 内递增,
内递增,
因为![]() ,
,
要![]() 存在唯一的零点
存在唯一的零点![]() ,且
,且![]() ,则
,则![]() ,
,
所以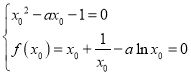 ,化简可得
,化简可得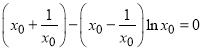 .
.
令![]() ,
,![]()
则![]()
所以![]() 在
在![]() 时单调递减,
时单调递减,
由题可知![]() ,
,![]() ,
,
而![]() ,
,
![]()
所以![]()
即![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】甲、乙两企业生产同一种型号零件,按规定该型号零件的质量指标值落在![]() 内为优质品.从两个企业生产的零件中各随机抽出了
内为优质品.从两个企业生产的零件中各随机抽出了![]() 件,测量这些零件的质量指标值,得结果如下表:
件,测量这些零件的质量指标值,得结果如下表:
甲企业:
分组 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
| 5 |
乙企业:
分组 |
|
|
|
|
|
|
|
频数 | 5 |
|
|
|
|
| 5 |
(1)已知甲企业的![]() 件零件质量指标值的样本方差
件零件质量指标值的样本方差![]() ,该企业生产的零件质量指标值X服从正态分布
,该企业生产的零件质量指标值X服从正态分布![]() ,其中μ近似为质量指标值的样本平均数
,其中μ近似为质量指标值的样本平均数![]() (注:求
(注:求![]() 时,同一组中的数据用该组区间的中点值作代表),
时,同一组中的数据用该组区间的中点值作代表),![]() 近似为样本方差
近似为样本方差![]() ,试根据企业的抽样数据,估计所生产的零件中,质量指标值不低于
,试根据企业的抽样数据,估计所生产的零件中,质量指标值不低于![]() 的产品的概率.(精确到
的产品的概率.(精确到![]() )
)
(2)由以上统计数据完成下面![]() 列联表,并判断能否在犯错误的概率不超过
列联表,并判断能否在犯错误的概率不超过![]() 的前提下认为两个企业生产的零件的质量有差异.
的前提下认为两个企业生产的零件的质量有差异.
甲厂 | 乙厂 | 总计 | |
优质品 | |||
非优质品 | |||
总计 |
附:
参考数据:![]() ,
,
参考公式:若![]() ,则
,则![]() ,
,
![]() ,
,![]() ;
;

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
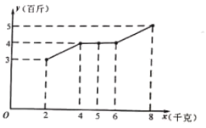
【题目】某公司的营销部门对某件商品在网上销售情况进行调查,发现当这件商品每回馈消费者一定的点数,该商品每天的销量就会发生一定的变化,经过统计得到以下表:
![]()
(1)经分析发现,可用线性回归模型拟合该商品销量![]() (百件)与返还点数
(百件)与返还点数![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测若返回6个点时该商品每天销量;
,并预测若返回6个点时该商品每天销量;
(2)该公司为了在购物节期间对所有商品价格进行新一轮调整,随机抽查了上一年购物节期间60名网友的网购金额情况,得到如下数据统计表:
网购金额 (单位:千元) |
|
|
|
|
|
| 合计 |
频数 | 3 | 9 | 9 | 15 | 18 | 6 | 60 |
若网购金额超过2千元的顾客定义为“网购达人”,网购金额不超过2千元的顾客定义为“非网购达人”.该营销部门为了进步了解这60名网友的购物体验,从“非网购达人”、“网购达人”中用分层抽样的方法确定10人,若需从这10人中随机选取3人进行问卷调查.设![]() 为选取的3人中“网购达人”的人数,求
为选取的3人中“网购达人”的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式及数据:①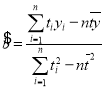 ,
,![]() ;②
;②![]() .
.