题目内容
已知⊙O的方程是x2+y2-2=0,⊙O′的方程是x2+y2-8x+10=0.由动点P向⊙O和⊙O′所引的切线长相等,求动点P的轨迹方程.
设P(x,y),则x2+y2-2=(x-4)2+y2-6,即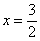 .
.
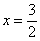 .
.由⊙O:x2+y2=2,⊙O′:(x-4)2+y2=6知两圆相离,切点分别为T、Q,则|PT|=|PQ|,如图.
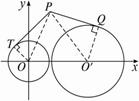
∵|PT|2=|PO|2-2,|PQ|2=|PO′|2-6,
∴|PO|2-2=|PO′|2-6.
设P(x,y),则x2+y2-2=(x-4)2+y2-6,即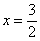 .
.

∵|PT|2=|PO|2-2,|PQ|2=|PO′|2-6,
∴|PO|2-2=|PO′|2-6.
设P(x,y),则x2+y2-2=(x-4)2+y2-6,即
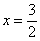 .
.
练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
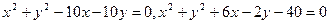 ,求(1)它们的公共弦所在直线的方程;(2)公共弦长。
,求(1)它们的公共弦所在直线的方程;(2)公共弦长。 ,则两圆x2+y2=r2与(x-1)2+(y+1)2=2的位置关系是( )
,则两圆x2+y2=r2与(x-1)2+(y+1)2=2的位置关系是( )  与
与 的位置关系是( )
的位置关系是( )