题目内容
一个盒子中有5只同型号的灯泡,其中有3只合格品,2只不合格品。现在从中依次取出2只,设每只灯泡被取到的可能性都相同,请用“列举法”解答下列问题:
(1)求第一次取到不合格品,且第二次取到的是合格品的概率;
(2)求至少有一次取到不合格品的概率。
(1)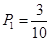 ;(2)
;(2)
解析试题分析:令三只合格灯泡分别为a,b,c,两只不合格灯泡分别为e,f,从中取出两只灯泡,所有的取法有ab,ac,ae,af,ba,bc,be,bf,ca,cb,ce,cf,ea,eb,ec,ef,fa,fb,fc,fe总的取法共二十种
(1)第一次取到不合格品,且第二次取到的是合格品取法有6种,分别为ea,eb,ec,fa,fb,fc,故概率是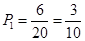 ;
;
(2)事件“至少有一次取到不合格品”的对立事件是“取到的全是正品”,“取到的全是正品”包括了六种分别为ab,ac,ba,bc,ca,cb,故事件“至少有一次取到不合格品”取法有14种,至少有一次取到不合格品事件的概率是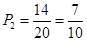
考点:本题考查了古典概率的求法
点评:本题主要考查随机事件、互斥事件等概率基础知识,考查运用概率知识解决实际问题的能力

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
(8分)对某校高一年级学生参加社区服务次数进行统计,随机抽取 名学生作为样本,得到这
名学生作为样本,得到这 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
| 分组 | 频数 | 频率 |
 | 10 | 0.25 |
 | 25 |  |
 |  |  |
 | 2 | 0.05 |
| 合计 | M | 1 |

⑴求出表中
 、
、 及图中
及图中 的值;
的值;⑵若该校高一学生有720人,试估计他们参加社区服务的次数在区间
 内的人数;
内的人数;⑶在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间
 内的概率.
内的概率.  ,且每个问题回答正确与否相互独立.
,且每个问题回答正确与否相互独立.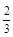 ,且每题正确完成与否互不影响。
,且每题正确完成与否互不影响。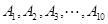 等10所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为
等10所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为 .
. 元,该同学决定按
元,该同学决定按 的分布列及数学期望.
的分布列及数学期望.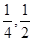 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为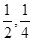 ;两人租车时间都不会超过四小时。
;两人租车时间都不会超过四小时。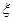 ,求
,求 .
.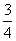 ,乙答对每个题的概率为
,乙答对每个题的概率为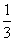 。
。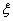 ,求
,求