Question

【题目】在四棱锥中，底面是边长为4的菱形，，，平面.

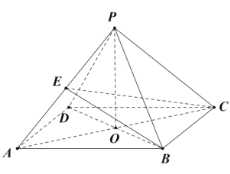
（1）证明：；

（2）若是的中点，，求二面角的余弦值.

Answer 1

【答案】（1）证明见解析；（2）.

【解析】

（1）根据底面为菱形，以及平面，可证得面，从而证明；

（2）方法一：利用线面垂直，作出二面角的平面角.在直角三角形中，逐步求出边长，最终求出线面角.

方法二：根据建立的空间直角坐标系，写出点的坐标后，代入公式计算即可．

（1）因为底面是菱形，所以.

又平面，平面，所以.

，所以面.

又面，所以.

（2）由（1）

在中，，∴，，

方法一：

过做于，连，则，

所以是二面角的平面角.

在中，，，

所以，即.

所以.

，

得，

，，

所以二面角的余弦值为.

方法二：

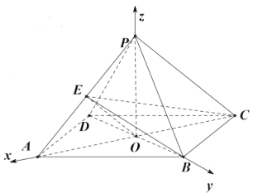
如图，以，，所在直线为，，轴，建立空间直角坐标系，

，，，，

，，.

设面的法向量为，

则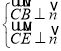，即，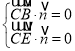

即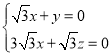，得方程的一组解为，，，

即.

又面的一个法向量为，

所以，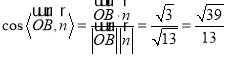

所以二面角的余弦值为.