题目内容
【题目】一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取![]() 个作为样本,称出它们的重量(单位:克),重量分组区间为
个作为样本,称出它们的重量(单位:克),重量分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,由此得到样本的重量频率分布直方图(如图).
,由此得到样本的重量频率分布直方图(如图).

(Ⅰ)求![]() 的值,并根据样本数据,试估计盒子中小球重量的众数与平均值;
的值,并根据样本数据,试估计盒子中小球重量的众数与平均值;
(Ⅱ)从盒子中随机抽取![]() 个小球,其中重量在
个小球,其中重量在![]() 内的小球个数为
内的小球个数为![]() ,求
,求![]() 的分布列和数学期望. (以直方图中的频率作为概率).
的分布列和数学期望. (以直方图中的频率作为概率).
【答案】(Ⅰ)![]() ,众数20,平均数24.6;(Ⅱ)分布列见解析,期望为
,众数20,平均数24.6;(Ⅱ)分布列见解析,期望为![]() .
.
【解析】
试题分析:(Ⅰ)由频率分布直方图中所有小矩形面积(频率)之和为1,可计算出![]() ,众数取频率最大即矩形最高的那个矩形的中点横坐标,平均值用各矩形中点值乘频率相加即得;(Ⅱ)
,众数取频率最大即矩形最高的那个矩形的中点横坐标,平均值用各矩形中点值乘频率相加即得;(Ⅱ)![]() 的可能取值为
的可能取值为![]() 、
、![]() 、
、![]() 、
、![]() ,利用样本估计总体,该盒子中小球重量在
,利用样本估计总体,该盒子中小球重量在![]() 内的概率为
内的概率为![]() ,因此有
,因此有![]() ,从而可得分布列,最后由期望公式可计算出期望.
,从而可得分布列,最后由期望公式可计算出期望.
试题解析:(Ⅰ)由题意,得![]() ,
,
解得![]() ;
;
又由最高矩形中点的的横坐标为20,可估计盒子中小球重量的众数约为20(克)
而![]() 个样本小球重量的平均值为:
个样本小球重量的平均值为:![]() (克)
(克)
故由样本估计总体,可估计盒子中小球重量的平均值约为![]() 克;
克;
(Ⅱ)利用样本估计总体,该盒子中小球重量在![]() 内的概率为
内的概率为![]()
则![]() .
.![]() 的可能取值为
的可能取值为![]() 、
、![]() 、
、![]() 、
、![]() ,
,
![]() ,
,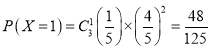 ,
,
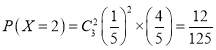 ,
,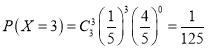 .
.
![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
![]() .(或者
.(或者![]() )
)

练习册系列答案
相关题目

