题目内容
已知函数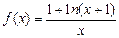
(Ⅰ)求函数f (x)的定义域
(Ⅱ)确定函数f (x)在定义域上的单调性,并证明你的结论.
(Ⅲ)若x>0时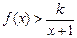 恒成立,求正整数k的最大值.
恒成立,求正整数k的最大值.
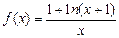
(Ⅰ)求函数f (x)的定义域
(Ⅱ)确定函数f (x)在定义域上的单调性,并证明你的结论.
(Ⅲ)若x>0时
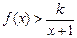 恒成立,求正整数k的最大值.
恒成立,求正整数k的最大值.(Ⅰ)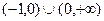 (Ⅱ)在(-1,0)和(0,+
(Ⅱ)在(-1,0)和(0,+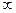 )上都是减函数
)上都是减函数
(Ⅲ)k的最大值为3
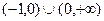 (Ⅱ)在(-1,0)和(0,+
(Ⅱ)在(-1,0)和(0,+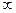 )上都是减函数
)上都是减函数(Ⅲ)k的最大值为3
(1)定义域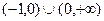
(2)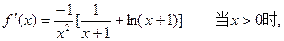
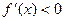 单调递减。
单调递减。
当 ,
,
令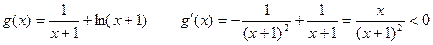
故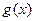 在(-1,0)上是减函数即
在(-1,0)上是减函数即 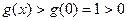 故此时
故此时
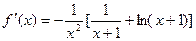
在(-1,0)和(0,+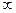 )上都是减函数
)上都是减函数
(3)当x>0时,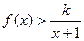 恒成立,令
恒成立,令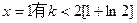
又k为正整数,∴k的最大值不大于3
下面证明当k=3时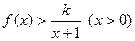 恒成立
恒成立
当x>0时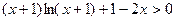 恒成立 令
恒成立 令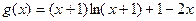
则
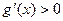
当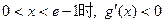
∴当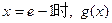 取得最小值
取得最小值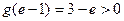
当x>0时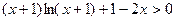 恒成立 因此正整数k的最大值为3
恒成立 因此正整数k的最大值为3
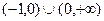
(2)
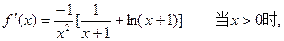
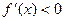 单调递减。
单调递减。当
 ,
,令
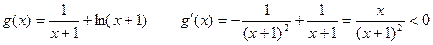
故
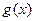 在(-1,0)上是减函数即
在(-1,0)上是减函数即 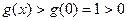 故此时
故此时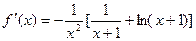
在(-1,0)和(0,+
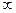 )上都是减函数
)上都是减函数(3)当x>0时,
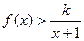 恒成立,令
恒成立,令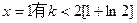
又k为正整数,∴k的最大值不大于3
下面证明当k=3时
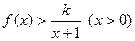 恒成立
恒成立当x>0时
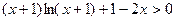 恒成立 令
恒成立 令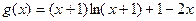
则

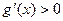
当
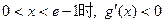
∴当
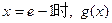 取得最小值
取得最小值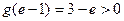
当x>0时
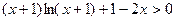 恒成立 因此正整数k的最大值为3
恒成立 因此正整数k的最大值为3
练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
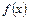 的导函数
的导函数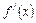 满足
满足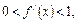 常数
常数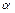 为方程
为方程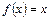
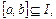 存在
存在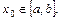 使等式
使等式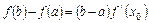 成立。 求证:方程
成立。 求证:方程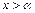 时,总有
时,总有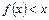 成立。
成立。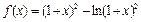 .
.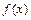 的单调区间;
的单调区间;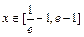 时,设函数
时,设函数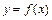 图象上任意一点处的切线的倾斜角为
图象上任意一点处的切线的倾斜角为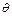 ,求
,求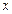 的方程
的方程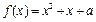 在区间[0,2]上恰好有两个相异的实根,求实数
在区间[0,2]上恰好有两个相异的实根,求实数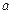 的取值范围。
的取值范围。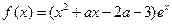 ,
,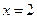 是函数
是函数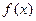 的一个极值点,求实数
的一个极值点,求实数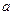 的值;
的值;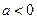 ,当
,当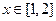 时,函数
时,函数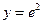 上方,求实数
上方,求实数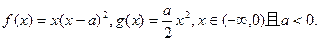
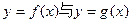 的图象的交点A的坐标;
的图象的交点A的坐标;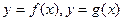 的图象在交点A处的切线分别为
的图象在交点A处的切线分别为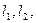 是否存在这样的实数a,使得
是否存在这样的实数a,使得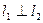 ?若存在,请求出a的值和相应的点A坐标;若不存在,请说明理由。
?若存在,请求出a的值和相应的点A坐标;若不存在,请说明理由。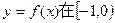 上最小值为F(a),求
上最小值为F(a),求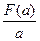 的最小值。
的最小值。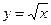 在
在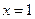 处的导数;
处的导数;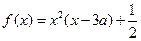 (
(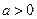 ,
,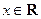 ).
).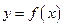 的极值;
的极值; (Ⅱ)若函数
(Ⅱ)若函数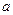 的取值范围.
的取值范围.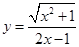 的导数是 ( )
的导数是 ( )



 ,
, ;
; ,
,