题目内容
已知点P(x,y)在由不等式组
确定的平面区域内,O为坐标原点,点A(-1,2),则|
|•cos∠AOP的最大值是 ( )
|
| OP |
分析:先画出 可行域,再根据点A的坐标及点P的坐标,将||
|•cos∠AOP的值表达为一个关于x,y的式子,即目标函数,然后将可行域中各角点坐标代入目标函数的解析式
| OP |
解答: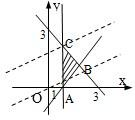 解:∵|
解:∵|
|•cos∠AOP=
=
(2y-x)
于是问题转化为求z=2y-x的最大值,
作出可行域如图所示,当直线经过点C(1,2)时,
z=2y-x取得最大值,zmax=2×2-1=3,
从而|
|•cos∠AOP的最大值为
故选B
 解:∵|
解:∵|. |
| OP |
| ||||
|
|
| ||
| 5 |
于是问题转化为求z=2y-x的最大值,
作出可行域如图所示,当直线经过点C(1,2)时,
z=2y-x取得最大值,zmax=2×2-1=3,
从而|
| OP |
3
| ||
| 5 |
故选B
点评:平面区域的最值问题是线性规划问题中一类重要题型,在解的关键是正确地画出平面区域,分析表达式的几何意义,然后结合数形结合的思想.

练习册系列答案
相关题目