题目内容
已知命题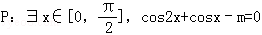 的否定为假命题,则实数m的取值范围是( )
的否定为假命题,则实数m的取值范围是( )
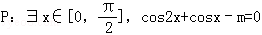 的否定为假命题,则实数m的取值范围是( )
的否定为假命题,则实数m的取值范围是( )A.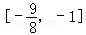 | B.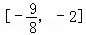 | C.[﹣1,2] | D.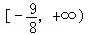 |
C
因为命题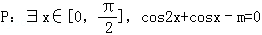 的否定为假命题,
的否定为假命题,
所以命题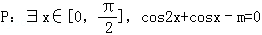 是真命题.
是真命题.
由cos2x+cosx﹣m=0,得m=cos2x+cosx=2cos2x+cosx﹣1=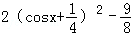 ,
,
∵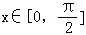 ,∴0≤cosx≤1,
,∴0≤cosx≤1,
∴当cosx=0时,m取得最小值﹣1;
当cosx=1时,m取得最大值2.
∴m的取值范围是[﹣1,2].
故选C.
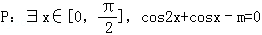 的否定为假命题,
的否定为假命题,所以命题
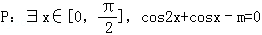 是真命题.
是真命题.由cos2x+cosx﹣m=0,得m=cos2x+cosx=2cos2x+cosx﹣1=
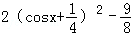 ,
,∵
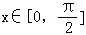 ,∴0≤cosx≤1,
,∴0≤cosx≤1,∴当cosx=0时,m取得最小值﹣1;
当cosx=1时,m取得最大值2.
∴m的取值范围是[﹣1,2].
故选C.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
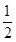 >0.则命题“p∧(
>0.则命题“p∧(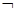 q)”是假命题;
q)”是假命题;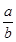 =-3;
=-3;
 ,
,  ,则
,则 =1;
=1;
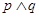 为真命题”是“命题
为真命题”是“命题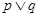 为真命题”的( )
为真命题”的( )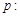 “
“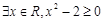 ”的否定形式是
”的否定形式是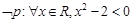 ;
;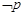 是
是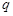 的必要条件,则
的必要条件,则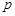 是
是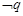 的充分条件;
的充分条件;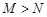 ”是“
”是“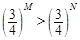 ”的充分不必要条件.
”的充分不必要条件.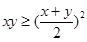 的充要条件
的充要条件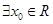 ,
,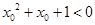 则
则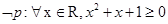
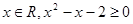 ”的否定是:“不存在
”的否定是:“不存在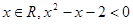 ”.
”.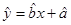 恒过样本中心
恒过样本中心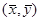 ,且至少过一个样本点.
,且至少过一个样本点. 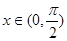 ,使
,使 .
.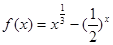 的零点在区间
的零点在区间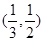 内.
内.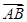 ·
·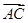 =
=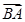 ·
·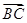 ,则|
,则|