题目内容
求下列各题的最值.(1)已知x>0,y>0,lgx+lgy=1,,求
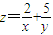 的最小值;
的最小值;(2)
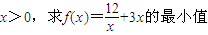 ;
;(3)
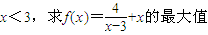 ;
;(4)
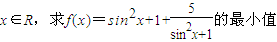 .
.
【答案】分析:(1)由lgx+lgy=1得xy=10,故可用基本不等式.
(2)由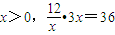 是常数,故可直接利用基本不等式
是常数,故可直接利用基本不等式
(3)因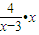 不是常数,故需变形.
不是常数,故需变形.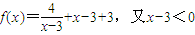 ,故需变号.
,故需变号.
(4)虽然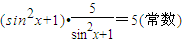 ,但利用基本不等式时,等号取不到,所以利用函数的单调性.
,但利用基本不等式时,等号取不到,所以利用函数的单调性.
解答:解:(1)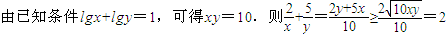 .
.
∴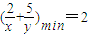 .当且仅当2y=5x,即x=2,y=5时等号成立.
.当且仅当2y=5x,即x=2,y=5时等号成立.
(2)∵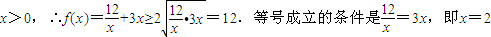 ,
,
∴f(x)的最小值是12
(3)∵x<3,∴x-3<0,∴3-x>0
∴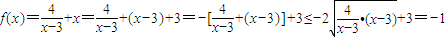 ,
,
当且仅当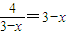 ,即x=1时,等号成立.故f(x)的最大值为-1.
,即x=1时,等号成立.故f(x)的最大值为-1.
(4)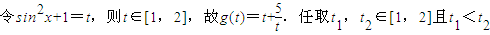 ,
,
则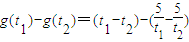
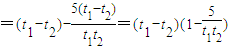
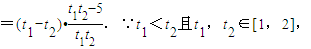
∴t1-t2<0,t1t2-5<0,故g(t1)-g(t2)>0,∴g(t1)>g(t2),
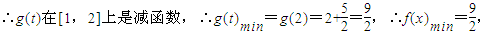
等号成立的条件是sin2x+1=2.sin2x=1,sin2x=±1,
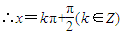
 .
.
点评:本题主要考查了基本不等式.在使用均值不等式时,要注意等号成立的条件.
(2)由
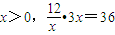 是常数,故可直接利用基本不等式
是常数,故可直接利用基本不等式(3)因
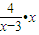 不是常数,故需变形.
不是常数,故需变形.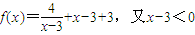 ,故需变号.
,故需变号.(4)虽然
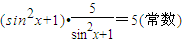 ,但利用基本不等式时,等号取不到,所以利用函数的单调性.
,但利用基本不等式时,等号取不到,所以利用函数的单调性.解答:解:(1)
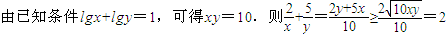 .
.∴
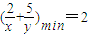 .当且仅当2y=5x,即x=2,y=5时等号成立.
.当且仅当2y=5x,即x=2,y=5时等号成立.(2)∵
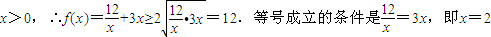 ,
,∴f(x)的最小值是12
(3)∵x<3,∴x-3<0,∴3-x>0
∴
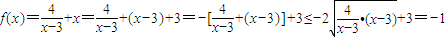 ,
,当且仅当
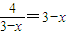 ,即x=1时,等号成立.故f(x)的最大值为-1.
,即x=1时,等号成立.故f(x)的最大值为-1.(4)
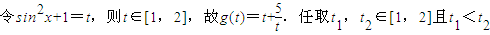 ,
,则
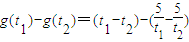
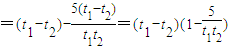
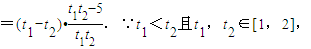
∴t1-t2<0,t1t2-5<0,故g(t1)-g(t2)>0,∴g(t1)>g(t2),
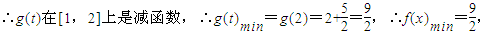
等号成立的条件是sin2x+1=2.sin2x=1,sin2x=±1,
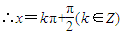
 .
.点评:本题主要考查了基本不等式.在使用均值不等式时,要注意等号成立的条件.

练习册系列答案
相关题目