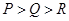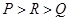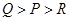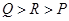题目内容
(8分)设a>b>c,求证：bc2+ca2+ab2<b2c+c2a+a2b.
见解析
利用综合法的思想证明不等式，作差后一定要化为因式乘积的形式
解：bc2+ca2+ab2-b2c-c2a-a2b
="b" (c2-a2)+b2(a-c)+ac(a-c)
=b(a+c)(c-a)-b2(c-a)-ac(c-a)
=(c-a)(c-b)(b-a)＜0
解：bc2+ca2+ab2-b2c-c2a-a2b
="b" (c2-a2)+b2(a-c)+ac(a-c)
=b(a+c)(c-a)-b2(c-a)-ac(c-a)
=(c-a)(c-b)(b-a)＜0
练习册系列答案
相关题目
；
;
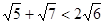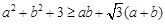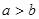，则下列不等式一定正确的是( )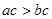
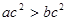
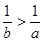
对
恒成立，则实数
的取值范围是 ．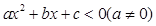
的解集为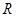
，那么（ ）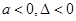
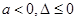
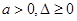
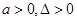
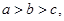求证：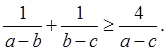
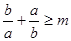恒成立，则m的取值范围是（ ）.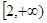
，
，
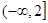
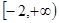
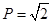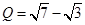，则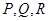
的大小顺序是( )
